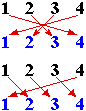
| Una permutazione di una sequenza di N oggetti può essere interpretata come una funzione iniettiva F da |  |
| Se P1 e P2 sono due permutazioni, possiamo chiamare loro prodotto la permutazione
| |
| (1) Descrivi come funzione la permutazione | |
| (2) L'insieme delle permutazioni di una sequenza di N oggetti dotato della operazione di moltiplicazione sopra descritta gode della proprietà commutativa? Ha un elemento neutro e, in caso affermativo, una operazione di passaggio all'inverso? | |
| (1) Come si vede bene sulla figura, P1 manda 1 in 4, poi P2 manda 4 in 1; analogamente 2 viene mandato in 3 e 3 poi in 4. La funzione che descrive 1 → 1, 2 → 4, 3 → 3, 4 → 2. | |
| (2) Questo prodotto non è commutativo. Ad esempio nel caso del precedente esempio 1 → 3, 2 → 2, 3 → 1, 4 → 4. Solo nel caso in cui N ≤ 2 il prodotto è commutativo (perché? …). Vi è, invece, l'elemento neutro: è la permutazione che lascia stare tutto com'è (ossia la funzione | 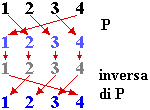 |
Per altri commenti:  calcolo combinatorio e strutture numeriche e non neGli Oggetti Matematici.
calcolo combinatorio e strutture numeriche e non neGli Oggetti Matematici.