La grandezza B è legata alla grandezza A secondo la relazione: B = A³ - 6 A² + 11 A. Nel caso in cui A = 2 ± 1 quanto vale B, ovvero qual è l'intervallo costituito dai valori di B al variare di A tra 2 – 1 e 2 + 1?

Per A = 1 e per A = 3 B  vale 6, ma ciò non significa che in tutto l'intervallo valga 6: ciò accadrebbe solo se ivi B fosse costante, e questo non può essere in quanto B varia come una funzione cubica di A.

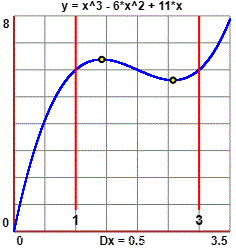
Dobbiamo studiare l'andamento di questa funzione. d(A3 - 6 A2 + 11 A) / dA = 3A2 - 12A + 11. È una quadratica con coefficiente direttivo positivo. La nostra funzione ha quindi pendenza negativa tra le due eventuali soluzioni di 3A2-12A+11 = 0; cerchiamole. 12/6 - √(122-3·4·11)/6 = 2 - 2√(62-3·11)/6 = 2 - √3/3 = 2 - 1/√3, 2 + 1/√3 B assume valore massimo in 2 - 1/√3 e valore minimo in 2 + 1/√3. Con un mezzo di calcolo ne determino i valori:   5.6151   6.3849 Concludo che per A in [1,3] B sta in [5.615…, 6.384…] che è contenuto in [5.6, 6.4]. Posso dire che per A = 2 ± 1  B = 6.0 ± 0.4.