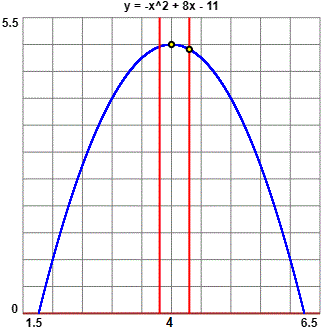
So che f(x) = −x² + 8x − 11. Se k sta tra 3.8 e 4.3 che cosa posso conludere di f(k)?

La funzione f non è crescente o decrescente nell'intervallo di indeterminazione di k, ma ha ivi un punto di massimo; più precisamente il suo massimo è in 4:  f'(x) = -2x+8 = 0 se x = 4. Dal grafico di f deduco che f(k) è compreso tra f(4) = 5 e f(4.3) = 4.91.

Il grafico tracciato con WolframAlpha, con  plot -x^2+8*x-11  e con  plot -x^2+8*x-11, 3.8 < x < 4.3

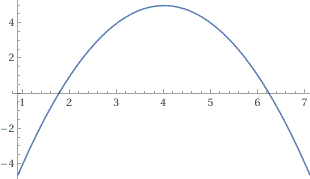
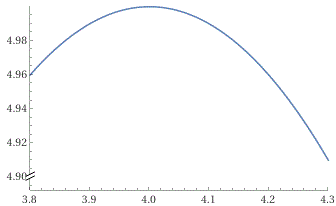
Posso usare anche un programmino in JavaScript (vedi):

function F(x) {return -x*x+8*x-11}
x1=3.8; x2=4.3
min=1e100; max=-1e100; n=1e7; h=(x2-x1)/n
for(i=0; i<=n; i=i+1) {
  x=x1+i*h; U=F(x)
  if(U<min) min=U; if(U>max) max=U } 
centro=min+(max-min)/2; raggio=(max-min)/2
document.write("min = "+min+"<br>max = "+max+"<br>"+centro+" +/- "+raggio)
            uscite:
min = 4.91
max = 5
4.955 +/- 0.04499999999999993

4.91 < f(k) < 5, ovvero f(k) = 4.955 ± 0.045

Posso fare un calcolo analogo anche con WolframAlpha:

minmax -x^2+8*x-11, 3.8 < x < 4.3
max{-x^2 + 8 x - 11 | 3.8<x<4.3} = 5 at x ≈ 4.
min{-x^2 + 8 x - 11 | 3.8<x<4.3} = 4.91 at x = 4.3