Cognome Nome

________________________________

classe

__________________

L'infinitamente grande e l'infinitamente piccolo

Scheda 1

Si usano spesso, nel linguaggio comune e in varie discipline (in Fisica, Filosofia, Astronomia, …) termini come "infinito" e "infinitesimo". Ma, con esattezza, che cosa vogliono dire? E, quando li si usa in Matematica, viene dato a loro lo stesso significato? Quali calcoli e altre manipolazioni matematiche si possono fare con questi "oggetti" infiniti o infinitesimi? Quali cautele occorre prestare nel lavorare con essi?   Nel "percorso" che stiamo per intraprendere, di cui questa scheda è la prima tappa, cercheremo di precisare questi interrogativi e tenteremo di dar loro qualche prima risposta.

1. L'«infinito» nel linguaggio comune e non

In un vocabolario per l'aggettivo infinito troviamo questi tre significati:

1 senza limiti   2 non determinato, non definito   3 innumerevole.

[1]   Secondo voi, nelle frasi a lato l'aggettivo o il sostantivo "infinito" che vi compare a quale di queste tre accezioni è più vicino?

Infiniti ringraziamenti. Quel film era una noia infinita. Il tempo secondo me è infinito. Il modo infinito è spesso usato come sostantivo. Il tuo programma va avanti all'infinito, controlla le condizioni che hai messo nel comando "if-then-else".

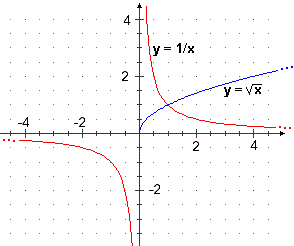
[2]   Viene chiamato "infinito" il simbolo ∞ che si usa nella indicazione di alcuni intervalli di numeri, come nei seguenti esempi, riferiti ai grafici a fianco. Secondo voi, "infinito" in questo caso a quale dei tre significati è più vicino? la funzione √ ha [0, ∞) come dominio la funzione reciproco (che a x associa 1/x) ha (–∞,0) U (0,∞) come dominio

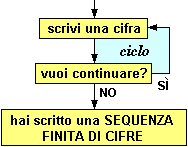	Un numero naturale è formato da una sequenza finita di cifre. Scrivo una cifra; se voglio scrivo a destra un'altra cifra; e così via. Quando mi fermo posso esprimere con una parola il numero che ho scritto. Il diagramma a sinistra illustra questo procedimento.
	[3]   Usa il diagramma scrivendo come prima cifra 2, poi 0, poi 2, … (alternando 2 e 0) e percorri il ciclo passando per la freccia "sì" in tutto quattro volte. Scrivi in lettere il numero che hai generato.   ________________________________________

    Quando dico che l'insieme dei numeri naturali pari (i numeri 0, 2, 4, 6, 8, 10, 12, …) è infinito intendo dire che i numeri pari sono in quantità "innumerevole", ovvero che non riesco a contarli tutti.
    Anche l'intervallo di numeri reali [0, ∞) è un insieme infinito: basti pensare che contiene l'insieme dei numeri pari. È anche un intervallo illimitato: comunque prenda un punto sull'asse x a destra dell'origine, ne posso tracciare uno a distanza doppia dall'origine, uno a distanza tripla, …: non esiste distanza oltre la quale non possa andare (eventualmente aggiungo un altro foglio, se non mi basta il pezzo di asse x che ho disegnato sul foglio che ho a disposizione).
    Anche (-∞, 0] è illimitato: comunque prenda un punto a sinistra dell'origine, ne posso trovare alla sua sinistra uno a distanza doppia, tripla, … .  Possiamo dire che [0, ∞) è superiormente illimitato e che (-∞, 0] è inferiormente illimitato.

[4]   Il diagramma a destra illustra il significato di numero reale. Usalo per generare un particolare numero reale nel seguente modo: –  non scrivere "–", –  scrivi "41", –  scrivi "." e poi –  percorri il ciclo scrivendo via via la cifra finale dei secondi che di volta in volta leggi sul tuo orologio.       [quando sei stanco fermati] • Puoi esprimere con una parola il numero che stai scrivendo? • Quanti sono i numeri reali che iniziano con "41."? • L'intervallo di numeri reali [41, 42] è limitato o illimitato? finito o infinito?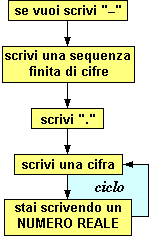

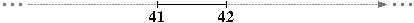2. L'infinito in matematica

In matematica il termine infinito viene usato in molti modi; ad es.:

per indicare gli estremi di un intervallo di numeri illimitato, senza confini invalicabili ("i numeri compresi tra 0 e infinito") per indicare un processo che si sviluppa stato dopo stato senza fine ("quel programma contiene un ciclo infinito") per indicare un insieme formato da una quantità innumerevole di oggetti ("i numeri reali compresi tra 0 e 1 sono infiniti")

Sono significati simili ai significati 1 e 3 del vocabolario della lingua italiana considerato nella prima sezione. E sono significati abbastanza collegati tra di loro: • quando dico che un insieme è infinito (significato C) intendo dire che il procedimento di conta dei suoi elementi, "1, 2, 3, …", è infinito (significato B). • un intervallo di numeri reali del tipo [k, ∞) (significato A) è sicuramente infinito (significato C), in quanto altrimenti avrebbe un ultimo elemento, che costituirebbe un confine oltre il quale non si potrebbe andare.

    Ma questi legami tra i diversi significati e la nostra intuizione, che è abituata a ragionare sul "finito", a volte ci possono trarre in inganno.   Abbiamo visto ad esempio che l'intervallo di numeri reali [41, 42], così come [0, 1] e ogni intervallo che ha per estremi numeri reali diversi, pur essendo limitato, è infinito:  presi comunque un tot di numeri che stanno nell'intervallo ne posso sicuramente trovare uno nuovo, che da un certo punto in poi abbia uno sviluppo delle cifre diverso dagli altri. Del resto, presi comunque due numeri x e y che stanno nell'intervallo, posso, proprio perché si tratta di un intervallo, trovarne un terzo compreso strettamente tra essi; basta, ad esempio prenderne la media: (x+y)/2.
   Vediamo qualche altro problema connesso all'uso dell'infinito.

3. Processi infiniti

[5]   Esegui "a mano" il risultato della divisione tra 6 e 9. Quale è il numero reale che ne è il risultato esatto? Prova a moltiplicare "a mano" per 3 questo numero; come fai? che cosa ottieni?

(1)
    6 | 9
      |————
      |

(2)
    6 | 9
      |————
      | 0

(3)
    6 | 0
    0 |————
      | 0

(4)
    6 | 9
   -0 |————
   —— | 0
    6

(5)
    6 | 9
   -0 |————
   —— | 0.6
    60

(6)
    6 | 9
   -0 |————
   —— | 0.6
    60
   -54
   ———
     6

(7)
    6 | 9
   -0 |————
   —— | 0.66
    60
   -54
   ———
     60

   ecc.

(7)—>(8) come (5)—>(6)

(8)—>(9) come (6)—>(7)

[6]   Batti un numero positivo qualunque sulla tua calcolatrice e poi, schiaccia ripetutamente il tasto per il calcolo della radice quadrata. Che cosa osservi? Secondo voi, si può sintetizzare con una formula quanto avete osservato?

4. Insiemi infiniti

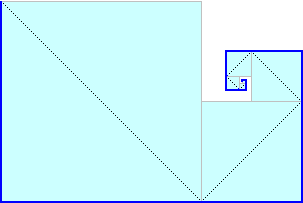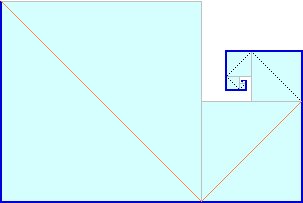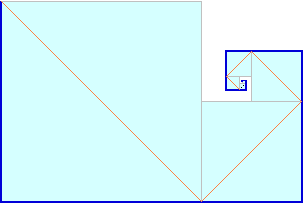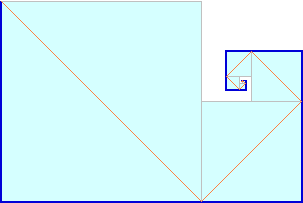
[7]   Siamo nella città sede delle prossime Olimpiadi. Gli hotel Jolly, Star ed Eden, identici, hanno tutti e tre una infinità di stanze che sono numerate  1, 2, 3, … .
• Il proprietario dello Star pensa: «Arriveranno molti turisti; attrezzo ad albergo anche il piccolo edificio a fianco: se completo l'edificio principale avrò altre 10 stanze per altrettanti nuovi clienti»
• Quello dell'Eden fa le cose in grande: «Costruisco un edificio uguale al precedente: sarò in grado di raddoppiare il numero dei clienti ospitati»
• Il proprietario del Jolly, invece pensa così: «Che stupidi! anche con l'hotel al completo si possono sempre operare dei cambiamenti di stanza degli ospiti e liberare posti per i nuovi arrivati»
    Sotto vedete raffigurati i tre hotel dopo i lavori di ampliamento. Il Jolly è praticamente contenuto strettamente sia nello Star che nell'Eden. Secondo voi ha ragione il suo proprietario a sostenere che potrà ospitare la stessa quantità di clienti? Come potrebbe fare?

Jolly	Star	Eden

Un problema a cui pensare a casa

[8]   Un raggio di luce, leggermente inclinato rispetto al piano orizzontale, entra nella infinita "spirale" di specchi raffigurata sotto (a destra è vista dall'alto). Il primo tratto rettilineo percorso nella spirale è lungo 1 m, il secondo è lungo 1/2 m, il terzo 1/4 m, il quarto 1/8 m, …. Secondo te prima o poi il raggio di luce esce da questo "percorso guidato"?  Con quale eventuale direzione?