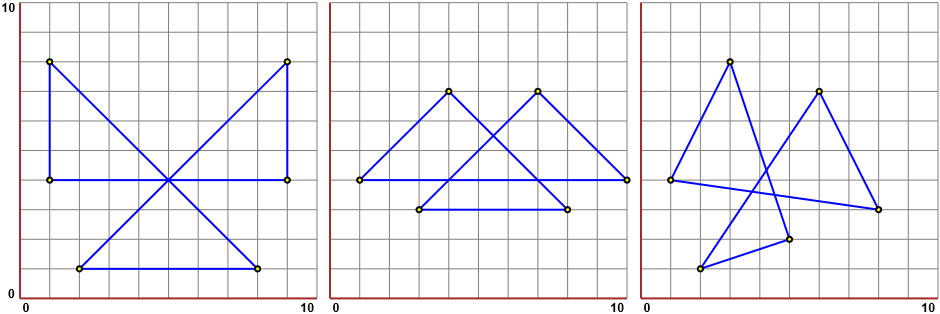
Nel triangolo a sinistra gli angoli segnati hanno somma 360°.  In quello al centro la loro somma è (90·2+45·4)°, ovvero nuovamente 360°.  E in quello a destra?

Invece che misurare gli angoli con un goniometro usiamo uno script che ci consente di ottenere l'ampiezza di un angolo ABC a partire dalle coordinate di A, B e C (angolo ottenuto ruotando la semiretta BA in senso antiorario sino alla semiretta BC). È lo script angolo presente qui.  Ecco, ad esempio, che cosa si ottiene per l'angolo a destra, quello che ha (8,3) come vertice B:

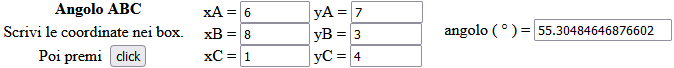
Analogamente calcolo le ampiezze in gradi di tutti e 6 gli angoli e ottengo:

Siamo quasi sicuri che in ogni caso la somma è 360°.  Come dimostrarlo?

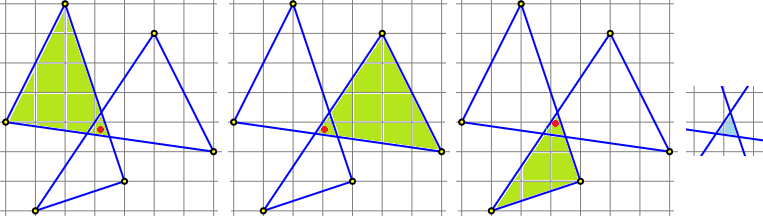
I tre triangoli sopra evidenzati hanno complessivamente 9 angoli con somma delle ampiezze pari a 180°·3.  I 6 angoli che ci interessano si ottengono togliendo da questi i tre angoli interni, che sono gli angoli di un triangolino, e quindi hanno come somma 180°.  Quindi i 6 angoli in tutto misurano 180°·3-180° = 360°. In modo simile avrei ragionato nel caso in cui i triangoli non si fossero intreccati, come nella figura qui a destra: anche in questo caso i 6 angoli che ci interessano si ottengono togliendo dai tre triangoli tre angoli uguali agli angoli del triangolino interno.

Invece di questo script potevo usare, in modo meno semplice (dando in input le coordinate dei triangoli), WolframAlpha. Le figure sono state costruite con script analoghi a quelli presentati qui, in grafici. Potevano essere tracciate con WolframAlpa, col comando polygon.  Ecco lo script che traccia il terzo poligono.