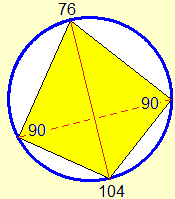
By doing a few experiments I understand that for a quadrilateral the equivalence between having opposite angles of amplitudes that have a sum of 180 ° and being inscribable in a circle holds.     Despite the evidence, how do I prove it?     We know that all angles inscribed in a circle that intercept the same arc on it have the same amplitude.  So I can trace back each configuration to a situation such as the one on the side, in which the upper and the lower part are two isosceles triangles and, therefore, the right and the left part are two equal right-angled triangles:  half of the opposite angles (those that in the figure are 76° and 104° wide) therefore they have a sum of 180°−90°, that is 90°.  Therefore the opposite angles certainly have a sum equal to 90°·2, that is 180°.

Come posso tracciare figure come quelle presenti nel testo del quesito mediante WolframAlpha con comandi come il seguente: polygon (cos(30°),sin(30°)), (cos(70°),sin(70°)), (cos(190°),sin(190°)), (cos(310°),sin(310°)), circle center(0,0) radius 1 Per avere anche le ampiezze degli angoli traccio solo il poligono: polygon (cos(30°),sin(30°)), (cos(70°),sin(70°)), (cos(190°),sin(190°)), (cos(310°),sin(310°)) Ottengo gli angoli, in radianti: interior angles | 2.094 rad | 1.745 rad | 1.047 rad | 1.396 rad Posso verificare che:     2.094 + 1.047 = 3.141    1.745 + 1.396 = 3.141