Sul teorema limite centrale
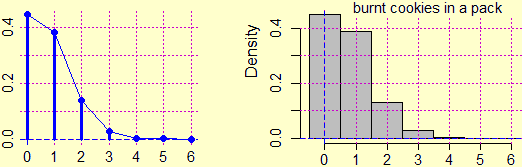
Supponiamo che una fabbrica di biscotti disponga di un forno che bruciacchi i biscotti con la frequenza p (ossia questa è la probabilità che un biscotto sia bruciacchiato) e che venda i biscotti in confezioni da n pezzi. Qual è la probabilità che in una confezione il numero N dei biscotti bruciacchiati sia k?
Se n = 6 e p = 1/8 la probabilità che esattamente i primi 4 biscotti siano bruciacchiati è (1/8)·(1/8)·(1/8)·(1/8)·(7/8)·(7/8) = (1/8)4·(7/8)2. Questo valore dobbiamo moltiplicarlo per i possibili sottoinsiemi di 4 elementi che possono essere formati da un insieme di 6 elementi:
C(6,4) = (6·5·4·3)/(4·3·2·1) = 6/4·5/3·4/2·3/1 = 6·5/2/1 = 3·5 = 15
Dunque, nel nostro caso particolare, la probabilità che vi siano 4 biscotti bruciacchiati è C(6,4)·(1/8)4·(7/8)2 = 15·(1/8)4·(7/8)2 = 0.0028038 = 0.28% (arrotondando). Procedo analogamente per gli altri valori di k.

In generale:
Pr(N = k) = C(n, k) · pk · (1 – p)n–k
Il calcolo con questa calcolatrice

Questa legge di distribuzione viene chiamata legge di distribuzione binomiale (o di Bernoulli). Si applica a tutte le situazioni in cui si ripete n volte la prova su una variabile casuale che può assumere solo due valori, in cui p è la probabilità di uno di questi due valori e N è il numero delle volte in cui questo valore esce.
Un altro esempio d'uso: in una certa popolazione di individui adulti di una data regione si sa che una particolare malattia infantile ha colpito in media 1 persona su 8; prese del tutto a caso 100 persone adulte di quella regione qual è la probabilità che non più di 10 siano state colpita da essa?
Potremmo fare il calcolo con la stessa calcolatrice:
Calcolo Binom(100,0) = 0.0000015878347497057898, ..., Binom(100,10) = 0.09730378495248684 e poi

0.0000015878347497057898, 0.00002268335356722557, 0.00016040371451109508, 0.000748550667718444, 0.0025931933845960375, 0.007112758997749131, 0.016088383447289703, 0.030863429470310868, 0.05125533822748053, 0.0748490653480668, 0.09730378495248684
La probabilità è del 28.1%
Ma, per chi sappia un po' programmare, è molto più semplice fare direttamente tutto il calcolo in JavaScript:
Q=0; P=1/8; n=100
for(k=0; k<11; k=k+1)
{ c=1; for(i=0; i<k; i=i+1) { c=c*(n-i)/(k-i) }
Q = Q + c*Math.pow(P,k)*Math.pow(1-P,n-k) }
document.write(Q*100,"%")
Output:
0.28099917939852637%
Ecco qualche grafico. Il primo rappresenta la binomiale con p = 0.2 e n = 5. Gli altri rappresentano quelle per p = 0.2 e n = 10, n = 30.
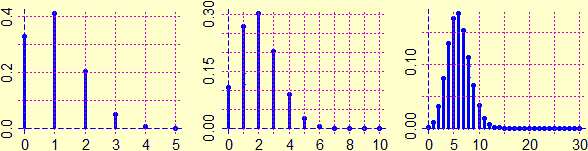
Si noti come all'aumentare di n l'istogramma di distribuzione tende ad assumere una forma simile alla gaussiana. Come mai? La binomiale di ordine n è ottenibile come somma di n termini uguali ad una variabile casuale ad uscite in 0 ed 1 (ad esempio, nel caso dei 6 biscotti, è la somma di 6 variabili ad uscite in 0 od 1).
Si può dimostrare che se Ui (i intero positivo) sono n variabili casuali (numeriche)
indipendenti con la stessa legge di distribuzione, allora
al crescere di n la variabile casuale
| ( | (x1– m)2 + (x2– m)2 + … (xn– m)2 | ) | 1/2 |
| ——————————————— | |||
| n−1 |
Ovvero,
al crescere di n la variabile casuale
| ( | (x1– m)2 + (x2– m)2 + … (xn– m)2 | ) | 1/2 |
| ——————————————— | |||
| n·(n−1) |
Il primo "σ" è la deviazione standard (sd nella nostra calcolatrice), il secondo è la deviazione standard della media (sigma nella calcolatrice).
Sotto a sinistra il grafico della gaussiana e il richiamo della sua definizione e di alcune sue proprietà.
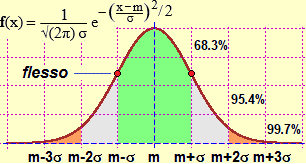
La proprietà ora richiamata costituisce il teorema limite centrale, che intreccia la probabilità e la statistica ed è alla base di tutte le applicazioni di quest'area della matematica. Un primo aspetto è che il fatto che la media di pressoché tutti i fenomeni casuali, comunque siano distribuiti, abbia andamento gaussiano ci consente di stimare la precisone della media ottenuta o, nel caso si stia simulando un fenomeno, la precisone della probabilità di esso.
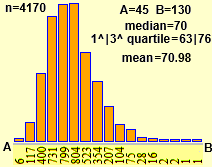
Un esempio. Sopra a destra è riprodotto l'istogramma di distribuzione dei
pesi (in kg) registrati in Italia al primo contingente delle visite di leva nel 1987 (4170 visite), che, come è evidente, non ha andamento gaussiano
(al di là di ciò che viene fatto credere spesso agli alunni, la distribuzione gaussiana non si presenta spesso in natura:
si distribuiscono grosso modo in tale maniera le altezze delle persone adulte di un dato sesso appartenti ad un certo gruppo razziale,
le lunghezze di una certa specie di pesci, …, una durata temporale registrata a mano da diverse persone con dei cronometri di precisione, …).
Il peso medio è di 70.98 kg. Se in quello stesso anno avessimo preso altri campioni di giovani maschi di quell'età, ciascuno di 4170 persone,
avremmo ottenuto valori medi diversi. Che cosa devo prendere come peso medio dell'intero insieme di giovani?
Facciamo i calcoli, poi daremo le spiegazioni.
Posso copiare i dati e inserirli nello script istogramma
Oltre al precedente istogramma ottengo:
n = 4170 minimo = 48 massimo = 126
1^ quarto: 63, 3^ quarto: 76 mediana (2^ quarto, a meta' dei dati ordinati) = 70
media = 70.47673860911272
Essendo i dati dei pesi troncati ai chilogrammi alla media devo aggiungere 0.5: media = 70.97673860911272 ≈ 70.977
Poi inseriamo i dati nella nostra calcolatrice2

e otteniamo:
mean = 70.47673860911272 (≈ 70.977) sigma = 0.16309161244207027 (≈ 0.163) 3*sigma = 0.4892748373262108 (≈ 0.489)
I dati erano N = 4170 e la loro media m = 70.977. Se ripetessi la prova con N altri individui
della stessa categoria presi a caso otterei altri valori della media che comunque
si distribuirebbero secondo una gaussianacon σ = 0.163.
Posso concludere che al 68.3%, nel 1987, il peso medio (in kg) di un
italiano maschio della stessa età è 70.977±0.163, al 99.7% (ossia con pratica certezza) è
70.977±0.163·3 = 70.977±0.489, ovvero 71±0.5 kg.
Altro esempio: se con un apparato misuratore ad alta sensibilità ottengono le 7 misure (in una data unità di misura) 7.3, 7.1, 7.2, 6.9, 7.2, 7.3, 7.4, posso calcolarne la media (7.2000…), la deviazione standard (0.061721) e il suo triplo (0.185), e concludere che il "valore vero" della misura al 99.7% 7.200±0.185.
Anche per valutare gli esiti di una simulazione si usa
questa proprietà. Vediamo che cosa si può ottenere:
Qual è la probabilità (estraendo 10 carte da un mazzo da 40) di avere almeno un tris (cioè 3 o 4 carte dello stesso valore)?
Si può ottenere, con 107 prove, al 99.7%, (38.436±0.047)% ovvero (38.44±0.05)%.
Notiamo che viene chiamata legge dei grandi numeri una
conseguenza del teorema limite centrale:
nelle stesse ipotesi del teorema, la media