•  Vi sono molti modi per descrivere questa ellisse:

Uno, semplice, è basato sul fatto che le ellissi sono dei cerchi "schiacciati", ossia trasformati con una scala non monometrica (con una scala monometrica otterrei altri cerchi, che, a dire il vero, sono anch'essi delle ellissi). Per descivere la forma di un'ellisse basta indicare la lunghezza dei due assi (ossia della distanza massima e della distanza minima tra due punti dell'ellisse) o il rapporto tra di essi. Posso allora misurare (approssimativamente) i due assi e dire, ad esempio, che questa ellisse ha asse maggiore lungo 3.2 cm e asse minore lungo 2.6 cm, o che il rapporto tra i due assi è 16/13.

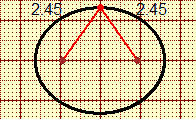
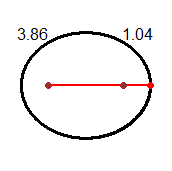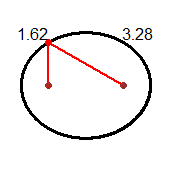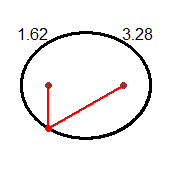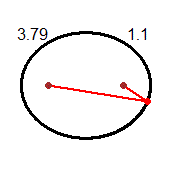
Un altro modo è calcolare gli assi "esattamente". L'asse maggiore è lungo 2.45*2, ovvero 3.86+1.04, ossia 4.9.

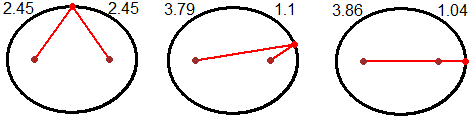
La distanza tra i fuochi è 4.9-1.04*2 = 4.9-2.08 = 2.82. Quindi, per il teorema di Pitagora, metà dell'asse minore è sqrt(2.45^2-(2.82/2)^2) = sqrt(4.0144) = 2.00360...
Quindi il rappotro tra i due assi è 4.9/(2*sqrt(4.0144)) = 1.22280... (16/13 = 1.2307...: OK).

•  Oppure potremmo tracciare l'ellisse, in vari modi. Primo modo.
Il semiasse maggiore è 4.9/2 = 2.45. Il semiasse minore è sqrt(2.45^2-1.41)^2). Usando ad esempio WolframAlpha (vedi), col comando
plot (x/2.45)^2+y^2/(2.45^2-1.41^2) = 1
ottengo la figura sotto a sinistra. Volendo posso sovrapporla alla figura originale (vedi sotto a destra) per confermare il risultato. WolframAlpha mi dà anche altre informazioni sull'ellisse, che confermano quanto trovato sopra.

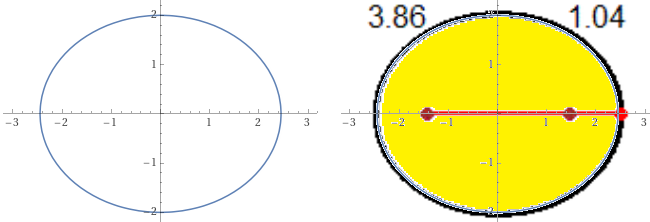
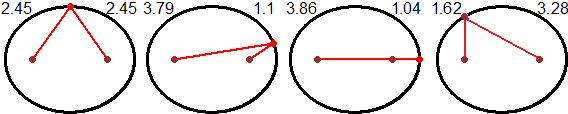
Altro modo:
ellipse, semiaxes 2.45, 2.0036, center (0,0)

Altro:
ellipse, foci (-1.41,0) and (1.41,0), semimajor axis 2.45

Posso descrivere l'ellisse anche in un modo ulteriore.

parametric plot  ( cos(t), sin(t) )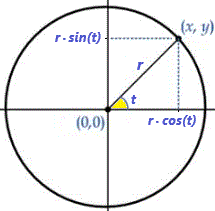

Un cerchio di raggio r centrato nell'origine posso descriverlo come l'insieme dei punti (r·cos(t), r·sin(t)) al variare del parametro t

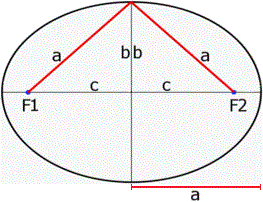c = 1.41 a = 2.45 b = 2.0036

La descrizione "parametrica" della nostra ellisse: parametric plot  ( a*cos(t), b*sin(t) )  for a = 2.45, b = 2.0036 Ottengo la stessa curva.

•  Naturalmente le descrizioni della nostra ellisse viste in precedenza sono descrizioni esatte di un'ellisse ideale: quella tracciata non corrisponde esattamente ad un'unica ellisse essendo tracciata con un tratto spesso ed essendo i valori indicati delle approssimazioni.  Per altri approcci allo studio della stessa curva l'esercizio 1a.10  QUI.