
Ricordiamo che le cosiddette combinazioni di n elementi k a k sono i sottoinsiemi di k elementi di un insieme di n elementi. Sono in quantità pari al numero delle sequenze di k elementi che posso formare diviso per il numero dei modi in cui posso ordinare queste sequenze, cioè:
n sequenze di k elementi n·(n-1)·…·(n-k+1) ——————————————————————————————— = ————————————————— n permutazioni di una sequenza k·(k-1)·…·1 |
n n-1 n-k+1
= —·———·…·—————
k k-1 1 |
| [il rapporto tra il prodotto dei primi k numeri interi positivi a scalare da n e il prodotto di quelli a scalare da k] |
| Questa quantità è indicata in vari modi: C(n,k), choose(n,k), |
| , … |
I valori C(n,k) sono calcolabili anche utlizzando il cosiddetto triangolo di Pascal (già noto 5 secoli prima di Pascal!), che richiamiamo usando WolframAlpha:

Sia dalla definzione che dalla precedente rappresentazione triangolare abbiamo che per calcolare
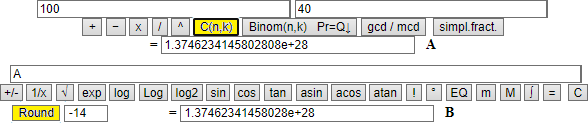
I valori di C(n,k) posso calcolarli automaticamente in molti modi. Vediamo ad esempio il calcolo di C(52,5) e di C(100,40). Con lo script coef binom ottengo:


Il secondo è un valore molto grande, che per tutti gli scopi pratici posso arrotondare, ad es., a 1.3476·1028.
Se mi interessassero tutte le cifre potrei usare WolframAlpha:
C(100,40) =
13746234145802811501267369720 = 1.374623414580281150126736972·1028
Come si vede lo script visualizza 17 cifre del valore, con le ultime 2 incerte a causa degli arrotondamenti. Potremmo usare direttamente lo script calcolatrice2, con cui potremmo effettuare automaticamente gli arrotondamenti (qui abbiamo arrotondato alla 14ª cifra prima del punto decimale: 13746234145802800000000000000)
Veniamo ai quesiti proposti.
• Quante sono le possibili mani di poker?
Ovvero, quanti sono i possibili insiemi di cinque carte che posso ricevere da un mazzo di 52 carte?
52 scelte possibili per la prima carta, 51 per la seconda, …, 48 scelte per la quinta. In tutto 52·51·50·49·48 modi di pescare le 5 carte. Ma non importa l'ordine con cui le pesco.
Gli ordini possibili sono 5·4·3·2. Quindi il numero di possibili di mani è:
(52·51·50·49·48) / (5·4·3·2) = 52·51·5·49·4
=
Ritroviamo il valore C(52,5) trovato prima.
• Un biologo deve fare un esperimento su 60 topi, scelti tra i 100 di cui dispone. In quanti modi può effettuare la scelta?
C(100,60) = C(100,40) = 100/40*99/39/*...61/1. Facendo i calcoli col computer, come visto prima, troviamo
1.374623·1028, ossia circa 1.4·1028.
Un numero enorme!
• x(0) = 1, x(n+1) = (y(n) + A/x(n)) / 2, x(n) → ?
Studiamo sperimentalmente, con A = 16, il limite di questa successione definita ricorsivamente; potremmo usare opportunamente la stessa calcolatrice, ma è molto più semplice usare un programmino, come questo realizzato in JavaScript:
A=16; x=1; for(n=0; n<=10; n=n+1) { document.write(x,", "); x=(x+A/x)/2 }
Output:
1, 8.5, 5.1911764705882355, 4.136664722546242, 4.002257524798522, 4.000000636692939, 4.000000000000051, 4, 4, 4, 4,
Proviamo con A = 0.25:
A=0.25; x=1; for(n=0; n<=10; n=n+1) { document.write(x,", "); x=(x+A/x)/2 }
Output:
1, 0.625, 0.5125, 0.5001524390243902, 0.5000000232305737, 0.5000000000000006, 0.5, 0.5, 0.5, 0.5, 0.5,
Si intuisce facilmente che il limite esista e sia √A. A questi punto studiamo la cosa teoricamente. Se il limite fosse L avremmo:
• Verifica col computer che per n intero positivo 1³ + 2³ + 3³ +…+ n³ = (n·(n+1) / 2)²
Con un programmino in JavaScript:
N=10; S=0; for(n=1; n<=N; n=n+1) { S=S+n*n*n
document.write(n,", ",S,", ",Math.pow(n*(n+1)/2,2),"<br>") }
Output:
1, 1, 1
2, 9, 9
3, 36, 36
4, 100, 100
5, 225, 225
...
10, 3025, 3025
Posso verificare la cosa con WolframAlpha: | 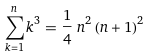 |
Un altro esempio:
• Studia la convergenza della successione x(0) = A, x(n+1) = √x(n)
Studiamo sperimentalmente, con ad es. A = 7, il limite della successione:
x=7; for(n=0;n<90;n=n+1) {x=Math.sqrt(x); document.write(x,", ") }
Output:
2.6457513110645907, 1.6265765616977859, 1.2753731068584542, 1.1293241814724655, ..., 1.0000000000000002, 1, 1, ...
Anche usando un qualsiasi altro numero positivo al posto di 1 si ottiene la convegergenza ad 1.