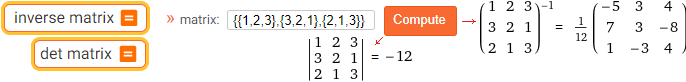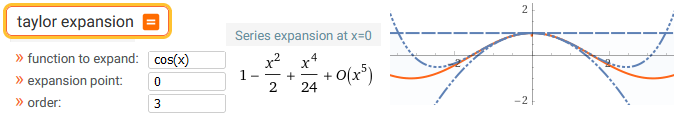
taylor expansion
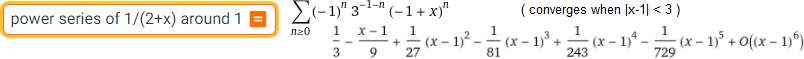
power series of 1/(2+x) around 1
Altro (chi è interessato ad approfondimenti ci scriva ...)
• La possibilità di approssimare intorno ad un punto tutte le funzioni più volte derivabili con funzioni polinomiali.
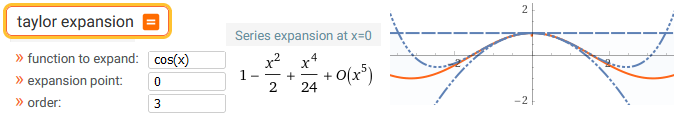
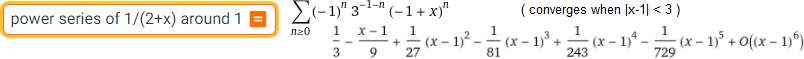
• La rappresentazione grafica di semplici funzioni a 2 input e 1 output reali, generalizzando casi di analoghe funzioni ad 1 input.
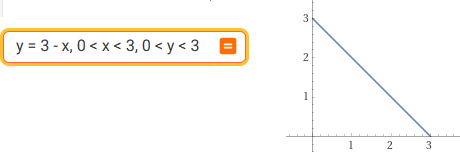
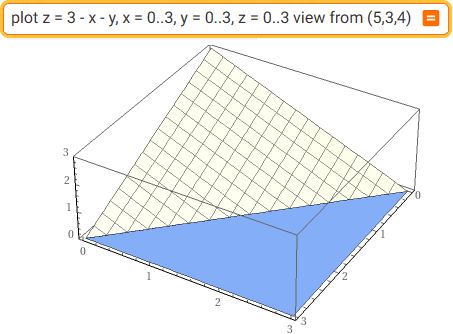
• La possibilità di collegare la lettura delle curve di livello delle carte geografiche alla rappresentazione grafica delle funzioni a 2 input.
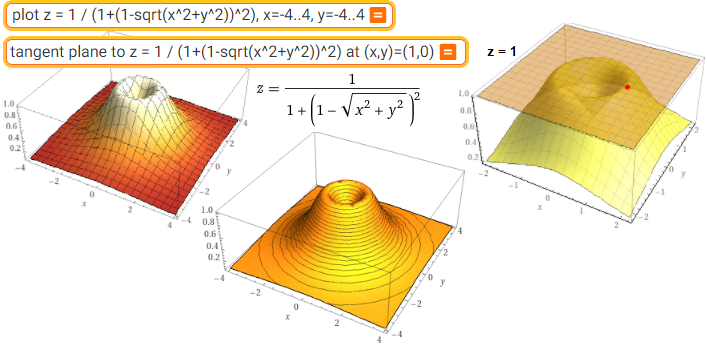
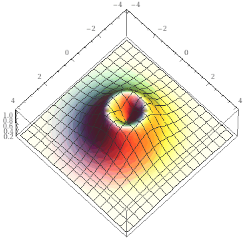 | plot z = 1 / (1+(1-sqrt(x^2+y^2))^2), x=-4..4, y=-4..4 view from (10,10,30) |
|
level curves 1 / (1+(1-sqrt(x^2+y^2))^2) level curves 1 / (1+(1-sqrt(x^2+y^2))^2), x=-2..2, y=-2..2 | 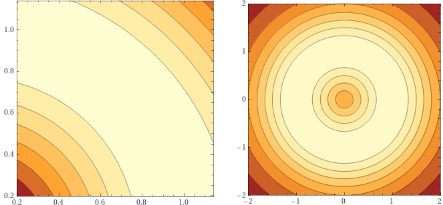 |
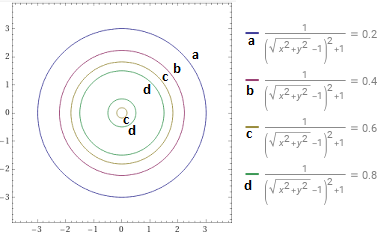
• Veniamo agli ultimi esempi, in ambito economico. L'economia è stata ed è tuttora l'ispiratrice di molte ricerche matematiche, e la matematica è uno strumento indispensabile per l'economia.
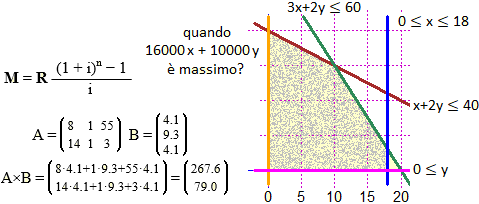
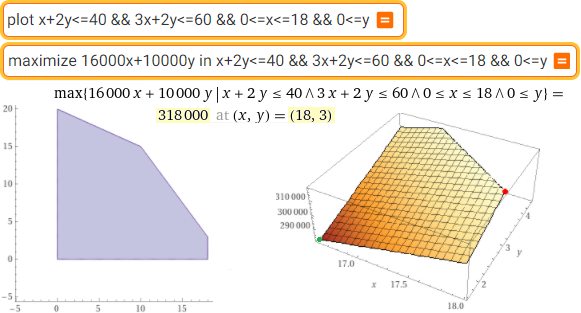
Primo esempio: la programmazione lineare, che serve per determinare l'allocazione (ripartizione e assegnazione) ottimale di risorse, disponibili in quantità limitata, per ottimizzare il raggiungimento di un obiettivo prestabilito (in condizioni di certezza, ossia in assenza di valutazioni casuali). Vediamo il problema illustrato sopra a destra.
Secondo esempio: la matematica finanziaria. Il caso sopra considerato nell'immagine è il calcolo del montante di una rendita immediata posticipata.
Tale montante è la somma dei montanti di ciascuna rata calcolati alla fine dell'ultimo periodo.
| M = R | (1 + i)n − 1 | ||
| ————— | |||
| i | |||
| M montante; R rata; i tasso; n num. rate. | |||
Ad un primo livello, la matematica finaziaria è un ottimo campo in cui mettere in uso ed esercitare
strumenti matematici elementari.
Approfondimenti possono essere trovati in
WolframAlpha (vedi gli esempi in
Money&Finance
e le voci
Mathworld subject actuarial mathematics,
Mathworld subject finance,
Mathworld subject economics,
MathWorld subject population dynamics).
Terzo esempio: il calcolo matriciale. Le matrici sono oggetto dell'algebra lineare e sono usate molto anche in geometria e in vari altri ambiti matematici, anche in ambito economico. Sono facili i concetti che intervengono per affrontare i primi elementi di calcolo matriciale. Noiose, e soggette a errori di calcolo, sono le manipolazioni delle matrici. Ai nostri giorni, capiti i procedimenti, ci si deve affidare al software. Esempi d'uso di WolframAlpha: