Programmare con JavaScript
Nelle pagine Internet, come questa, si possono inserire procedimenti di calcolo ("programmi") che consentono di fare elaborazioni di vario tipo. Questi procedimenti si chiamano "script". È il modo di realizzare programmi (in inglese chiamato anche "coding") più usato. Sotto vediamo un esempio. In altra parte del sito (vedi) sono presenti molti script già redatti, usabili a "scatola nera". Esplorando il codice sorgente di questi script (o di quelli presenti in quasi ogni pagina web: quando prenotiamo la presenza ad uno spettacolo, il posto in un albergo, un viaggio in treno o in aereo, ... usiamo degli script) possiamo farci una prima idea di questo linguaggio di programmazione. Ci possiamo fare anche un'idea di come faccia software sofisticato come WolframAlpha a elaborare le soluzioni: utilizza programmi simili a questi, anche se decisamente più complessi.
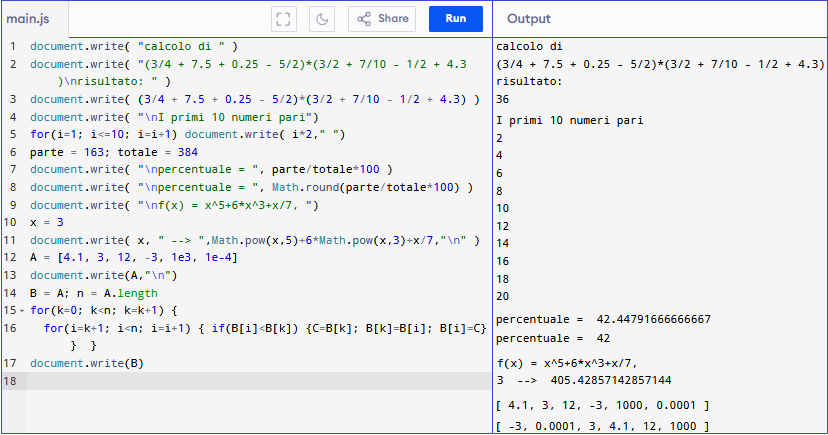
Facciamo ricorso a due dei molti siti in cui si possono provare ad eseguire degli script (e farsi un'idea concreta di che cosa vuol dire programmare), www.learnhindituts.com/online-javascript-compiler e www.programiz.com/javascript/online-compiler, che hanno due piccole differenze: nel primo si possono inserire alcuni comandi "html", nel secondo no. Qui metteremo esempi per entrambi i siti.
Negli esempi seguenti i comandi "html" inseriti sono <br> - break - che indica "a capo"; il comando che indica uno spazio bianco (in questa versione più spazi introdotti con " " nelle uscite vengono interpretati come uno solo); → che indica la freccia →.
Al loro posto (con la versione del secondo sito) possiamo usare \n (nuova riga), possiamo introdurre più spazi bianchi, possiamo indicare la freccia con "->".
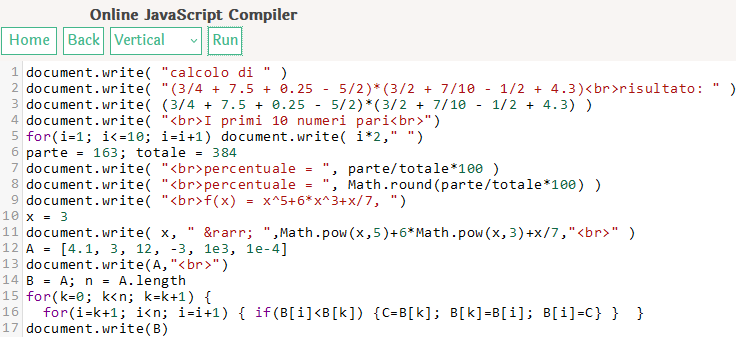
Ecco un primo programma, nelle due versioni. Si noti la presenza di "Math." in testa al nome di operazioni matematiche più complesse delle "4 operazioni", come sqrt - radice quadrata, pow - elevamento a potenza, round - arrotondamento, ...(vedi).
Nota. Si può fare tutto (anche le rappresentazioni grafiche) senza ricorrere ai siti citati. Vedi QUI.
Prima versione di Js:
document.write( "calcolo di " )
document.write( "(3/4 + 7.5 + 0.25 - 5/2)*(3/2 + 7/10 - 1/2 + 4.3)<br>risultato: " )
document.write( (3/4 + 7.5 + 0.25 - 5/2)*(3/2 + 7/10 - 1/2 + 4.3) )
document.write( "<br>I primi 10 numeri pari<br>")
for(i=1; i<=10; i=i+1) document.write( i*2," ")
parte = 163; totale = 384
document.write( "<br>percentuale = ", parte/totale*100 )
document.write( "<br>percentuale = ", Math.round(parte/totale*100) )
document.write( "<br>f(x) = x^5+6*x^3+x/7, ")
x = 3
document.write( x, " → ",Math.pow(x,5)+6*Math.pow(x,3)+x/7,"<br>" )
A = [4.1, 3, 12, -3, 1e3, 1e-4]
document.write(A,"<br>")
B = A; n = A.length
for(k=0; k<n; k=k+1) {
for(i=k+1; i<n; i=i+1) { if(B[i]<B[k]) {C=B[k]; B[k]=B[i]; B[i]=C} } }
document.write(B)


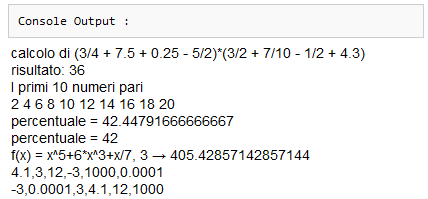
Seconda versione di Js:
document.write( "calcolo di " ) document.write( "(3/4 + 7.5 + 0.25 - 5/2)*(3/2 + 7/10 - 1/2 + 4.3)\nrisultato: " ) document.write( (3/4 + 7.5 + 0.25 - 5/2)*(3/2 + 7/10 - 1/2 + 4.3) ) document.write( "\nI primi 10 numeri pari\n") for(i=1; i<=10; i=i+1) document.write( i*2," ") parte = 163; totale = 384 document.write( "\npercentuale = ", parte/totale*100 ) document.write( "\npercentuale = ", Math.round(parte/totale*100) ) document.write( "\nf(x) = x^5+6*x^3+x/7, ") x = 3 document.write( x, " --> ",Math.pow(x,5)+6*Math.pow(x,3)+x/7,"\n" ) A = [4.1, 3, 12, -3, 1e3, 1e-4] document.write(A,"\n") B = A; n = A.length for(k=0; k<n; k=k+1) { for(i=k+1; i<n; i=i+1) { if(B[i]<B[k]) {C=B[k]; B[k]=B[i]; B[i]=C} } } document.write(B)
Nei calcoli per valori positivi oltre 10308 (meglio, per valori ≥ 21024) sia ha un overflow (infinito macchina), sotto a 10-323 (meglio, per valori positivi ≤ 2-1076) si ha un underflow (i valori vengono eguagliati a 0):
document.write(1e308,", ",1e309,", ",1e-323,", ",1e-324)
Output:
1e+308, Infinity, 1e-323, 0
Un altro esempio, l'ordinamento di parole invece che numeri:
A = ['casa','pino','cielo','zio','io','tu','zia','ala']
document.write(A,"<br>")
B = A; n = A.length
for(k=0; k<n; k=k+1) {
for(i=k+1; i<n; i=i+1) { if(B[i]<B[k]) {C=B[k]; B[k]=B[i]; B[i]=C} } }
document.write(B)
o document.write(A,"\n")
Output:
casa,pino,cielo,zio,io,tu,zia,ala
ala,casa,cielo,io,pino,tu,zia,zio
L'ordine di grandezza ("floor(x)" è la parte intera di x, "log10(x)" è il numero a cui elevare 10 per avere x):
x=10; y=9999; z=0.03
document.write("ordine di grandezza di ",x," = ",Math.floor(Math.log10(x)))
document.write("<br>ordine di grandezza di ",y," = ",Math.floor(Math.log10(y)))
document.write("<br>ordine di grandezza di ",z," = ",Math.floor(Math.log10(z)))
o senza <br>
Output:
ordine di grandezza di 10 = 1
ordine di grandezza di 9999 = 3
ordine di grandezza di 0.03 = -2
Come si misura il tempo?
In JS new Date assume il valore in millesecondi del tempo trascorso da un certo istante fissato a priori, non ci interessa quale. Per misurare il tempo che trascorre nell'esecuzione di un programma da un certo punto ad un altro basta che mettiamo nel primo punto ad esempio sec1=new Date e nel secondo sec2=new Date e stampiamo alla fine sec2-sec1. La cosa può essere utile per confrontare il tempo nell'esecuzione di due algoritmi e vedere quale è più veloce. Confrontiamo ad esempio il calcolo di questi due termini, algebricamente equivalenti:
| e |
|
Facciamo il calcolo (con due diversi programmini) molte volte, per avere dei tempi rilevabili facilmente (alla fine dividiamo per 1000 per avere i tempi in secondi):
n=5e5; x=1/3; for(j=0; j<10; j=j+1)
{n=n*2; sec1=new Date
for(i=0; i<n; i=i+1) y=5/(x+3)+2/(x+2)
sec2=new Date; document.write("s="+(sec2-sec1)/1000+" n="+n+"<br>") }
n=5e5; x=1/3; for(j=0; j<10; j=j+1)
{n=n*2; sec1=new Date
for(i=0; i<n; i=i+1) y=(7*x+16)/(Math.pow(x,2)+5*x+6)
sec2=new Date; document.write("s="+(sec2-sec1)/1000+" n="+n+"<br>") }
Mi forniscono:
s=0.014 n=1000000 s=0.03 n=2000000 s=0.058 n=4000000 s=0.117 n=8000000 s=0.238 n=16000000 s=0.469 n=32000000 s=0.957 n=64000000 s=1.896 n=128000000 s=3.797 n=256000000 s=7.57 n=512000000 | s=0.024 n=1000000 s=0.043 n=2000000 s=0.085 n=4000000 s=0.168 n=8000000 s=0.341 n=16000000 s=0.691 n=32000000 s=1.361 n=64000000 s=2.78 n=128000000 s=5.726 n=256000000 s=12.114 n=512000000 |
Il secondo termine, che magari a scuola siamo stati abituati a preferire, costa, in termini di tempo, circa il doppio del primo.
Come realizzare istogrammi (diagrammi a barre):
basta stampare uno stesso carattere (ad es. #) più volte; si può aumentare o diminuire la lughezza delle colonne modificando il valore assegnato a "lung" (il numero di # utilizzati in tutto):
lung=80 // modifica lung per avere istogramma piu' o meno lungo
dati = [127,585,430,1256,148]
n = dati.length; max=0
totale = 0; for(i=0; i<n; i=i+1) totale = totale+dati[i]
document.write(dati," - ISTOGRAMMA:<br>")
for(i=0; i<n; i=i+1) { p = Math.round(dati[i]/totale*lung);
for(k=1; k<=p; k=k+1) document.write("#");
document.write(" ",dati[i],"<br>") }
o
lung=80 // modifica lung per avere istogramma piu' o meno lungo
dati = [127,585,430,1256,148]
n = dati.length; max=0
totale = 0; for(i=0; i<n; i=i+1) totale = totale+dati[i]
document.write(dati," - ISTOGRAMMA:)
for(i=0; i<n; i=i+1) { p = Math.round(dati[i]/totale*lung);
s=""; for(k=1; k<=p; k=k+1) ) s=s+"#";
document.write(s, " ",dati[i] ) }
Output:
127,585,430,1256,148 - ISTOGRAMMA:
#### 127
################## 585
############## 430
####################################### 1256
##### 148
Con lung=150
127,585,430,1256,148 - ISTOGRAMMA:
####### 127
################################## 585
######################### 430
########################################################################## 1256
######### 148
Se ho una distribuzione percentuale con le percentuali arrotondate agli interi (come 29,23,12,8,21,7, la cui somma è cento) posso prendere lung=100
############################# 29 ####################### 23 ############ 12 ######## 8 ##################### 21 ####### 7
Se ho una distribuzione di 57 dati posso prendere lung=57 o lung=57*2
lung=57
document.write(
"ISTOGRAMMA alunni con pesi in kg in [55,60),[60,65),..,[95,100)<br>")
dati = [3,8,13,16,5,6,5,0,1]
n = dati.length; max=0
totale = 0; for(i=0; i<n; i=i+1) totale = totale+dati[i]
for(i=0; i<n; i=i+1) { p = Math.round(dati[i]/totale*lung);
for(k=1; k<=p; k=k+1) document.write("#");
document.write(" ",dati[i],"<br>") }
o
lung=57
document.write(
"ISTOGRAMMA alunni con pesi in kg in [55,60),[60,65),..,[95,100)")
dati = [3,8,13,16,5,6,5,0,1]
n = dati.length; max=0
totale = 0; for(i=0; i<n; i=i+1) totale = totale+dati[i]
for(i=0; i<n; i=i+1) { p = Math.round(dati[i]/totale*lung);
s=""; for(k=1; k<=p; k=k+1) s=s+"#";
document.write(s," ",dati[i]) }
ISTOGRAMMA alunni con pesi in kg in [55,60),[60,65),..,[95,100)
### 3
######## 8
############# 13
################ 16
##### 5
###### 6
##### 5
0
# 1
Con lung=57*2
###### 3
################ 8
########################## 13
################################ 16
########## 5
############ 6
########## 5
0
## 1
Altro esempio:
lung=500
document.write("ISTOGRAMMA morti nel 2006 per eta' negli intervalli delimitati da 0, 5, 10,..., 105, 110<br>")
dati = [43, 5, 6, 16, 23, 26, 28, 37, 56, 88, 141, 225, 350,
518, 814, 1245, 1771, 2027, 1643, 727, 195, 17]
n = dati.length; max=0
totale = 0; for(i=0; i<n; i=i+1) totale = totale+dati[i]
for(i=0; i<n; i=i+1) { p = Math.round(dati[i]/totale*lung);
for(k=1; k<=p; k=k+1) document.write("#");
document.write(" ",dati[i],"<br>") }
o
lung=400
document.write("ISTOGRAMMA morti nel 2006 per eta' negli intervalli delimitati da 0, 5, 10,..., 105, 110")
dati = [43, 5, 6, 16, 23, 26, 28, 37, 56, 88, 141, 225, 350,
518, 814, 1245, 1771, 2027, 1643, 727, 195, 17]
n = dati.length; max=0
totale = 0; for(i=0; i<n; i=i+1) totale = totale+dati[i]
for(i=0; i<n; i=i+1) { p = Math.round(dati[i]/totale*lung);
s=""; for(k=1; k<=p; k=k+1) s=s+"#";
document.write(s," ",dati[i]) }
Output:
ISTOGRAMMA morti nel 2006 per eta' negli intervalli delimitati da 0, 5, 10,..., 105, 110
## 43
5
6
# 16
# 23
# 26
# 28
## 37
### 56
#### 88
####### 141
########### 225
################# 350
########################## 518
######################################### 814
############################################################## 1245
######################################################################################### 1771
##################################################################################################### 2027
################################################################################## 1643
#################################### 727
########## 195
# 17
Un altro, la stampa dei numeri primi (k è divisibile per h se la divisione k/h è uguale al suo arrotondamento; AND è indicato da "&&")
// i numeri primi fino a N
N=300
for(k = 1; k <= N; k=k+1)
{ h=2;
while(h<k && k/h != Math.round(k/h) ) h=Number(h+1)
if(h==k) document.write(h," ")
}
o
N=300; s=""
for(k = 1; k <= N; k=k+1)
{ h=2
while(h<k && k/h != Math.round(k/h) ) h=Number(h+1)
if(h==k) s=s+Number(h)+" "
}
document.write(s)
Output:
2 3 5 7 11 13 17 19 23 29 31 37 41 43 47 53 59 61 67 71 73 79 83 89 97 101 103 107 109 113 127 131 137 139 149 151 157 163 167 173 179 181 191 193 197 199 211 223 227 229 233 239 241 251 257 263 269 271 277 281 283 293
Avessi voluto più spazio tra un'uscita e l'altra avrei usato: document.write(h," ") ottenendo: 2 3 5 7 11 ...
Un altro, una successione:
for(n=0; n<=9; n=n+1) document.write(n," → ",Math.pow(2,n)," ") o for(n=0; n<=9; n=n+1) document.write(n," -> ",Math.pow(2,n)," ")
Output:
0 → 1 1 → 2 2 → 4 3 → 8 4 → 16 5 → 32 6 → 64 7 → 128 8 → 256 9 → 512
Ovvero, per ricorsione:
x=1; for(n=0; n<=9; n=n+1) { document.write(x," "); x=x*2 }
Output:
1 2 4 8 16 32 64 128 256 512
Vedi QUI altri esempi di procedimenti ricorsivi.
Un altro, la scomposizione di un intero positivo in fattori primi, usando while ("fin tanto che").
La riga preceduta da // contiene commenti, senza effetti sulla esecuzione.
if ... ... else ... indica un "se ... allora ... altrimenti ..."
// scomposizione di N intero positivo in fattori primi
n=9632136; document.write("1"); k=2
while(k <= n) {
if(n/k == Math.round(n/k)) {n=n/k; document.write(", ",k)}
else k=k+1 }
o
n=9632136; k=2; s="1"
while(k <= n) {
if(n/k == Math.round(n/k)) {n=n/k; s=s+", "+k}
else k=k+1 }
document.write(s)
Output:
1, 2, 2, 2, 3, 37, 10847
Un altro, la radice quadrata di un numero positivo per "bisezione":
// radice quadrata di x
x = 76
// parto da un intervallo contenente la radice, [0,x] se x>1, [0,1/x] se no
a = 0; if(x > 1) {b = x} else {b = 1/x}
for(n=1; n < 60; n=n+1) {
m = (a+b)/2; y = m*m
if(y < x) {a = m} else {b = m}
document.write(" | ", m) }
o
x = 76; s=""
// parto da un intervallo contenente la radice, [0,x] se x>1, [0,1/x] se no
a = 0; if(x > 1) {b = x} else {b = 1/x}
for(n=1; n < 60; n=n+1) {
m = (a+b)/2; y = m*m
if(y < x) {a = m} else {b = m}
s=s+" | "+m }
document.write(s)
Output:
| 38 | 19 | 9.5 | 4.75 | 7.125 | 8.3125 | ... | 8.717797887081346 | 8.717797887081346
Se voglio direttamente la radice:
x = 76
a = 0; if(x > 1) {b = x} else {b = 1/x}
for(n=1; n < 100; n=n+1) {
m = (a+b)/2; y = m*m
if(y < x) {a = m} else {b = m} }
document.write(m)
Output:
8.717797887081346
Come risolvere, analogamente, un'equazione F(x) = 0 in un intervallo in cui F cambia segno.
Vediamo un esempio (4·sin(x)+1-x = 0) dopo aver tracciato il grafico (ad esempio con questo script):
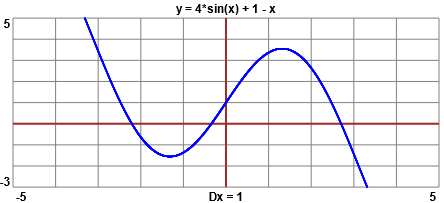
Una funzione G(t) = ... viene definita con comando del tipo G(t) {return ...}. Ecco il programma (prima troviamo la soluzione tra 1 e 4, poi tra -1 e 0 e tra -3 e -1):
function F(x) {return 4*Math.sin(x)+1-x }
a=1; b=4
if(F(a)*F(b)>0) document.write ("F(a) e F(b) hanno segno =")
else {
for(i=0; i<100; i=i+1) {
m = a+(b-a)/2; y1 = F(a); y2 = F(m); y3 = F(b)
if(y1*y2 > 0) {a = m} else {b = m} }
document.write(m)
}
Output: 2.70206137332604
a=-1; b=0 -> -0.3421850529244582
a=-3; b=-1 -> -2.210083944092661
Per vedere un altro esempio, consideriamo come si possono trovare il massimo e il minimo di una funzione in un intervallo I semplicemente calcolando molti valori presi a caso in I. Per generare a caso un numero tra 0 e 1 si usa il comando random(). Consideriamo la stessa funzione considerata sopra tra -2 e 3; dal grafico capisco che il minimo lo si ha circa in x = -1.5 e il massimo circa in x = 1.5. Lasciamo al lettore la comprensione del programma.
function F(x) {return 4*Math.sin(x)+1-x }
a=-2; b=3; h=b-a
if(F(a)>F(b)) {min=F(b);max=F(a);x1=b;x2=a} else {min=F(a);max=F(b);x1=a;x2=b}
for(i=1; i<=2e8; i=i+1) {x=Math.random()*h+a
if(F(x) < min) { min=F(x); x1=x }
if(F(x) > max) { max=F(x); x2=x } }
document.write("Circa:<br>")
document.write("minimo = ",min," per x = ",x1,"<br>")
document.write("massimo = ",max," per x = ",x2)
o senza "<br>"
Output:
Circa:
minimo = -1.5548672745545988 per x = -1.3181160775298748
massimo = 3.554867274554599 per x = 1.3181160782404162
I valori sono scelti casualmente. Se ripeto la prova ottengo valori leggermente diversi:
minimo = -1.5548672745545988 per x = -1.3181160786913257 massimo = 3.5548672745545993 per x = 1.3181160694116283
Posso prendere: min = -1.554867274554599 in -1.31811607, max = 3.554867274554599 in 1.31811607
Controlliamo le soluzioni con WolframAlpha:
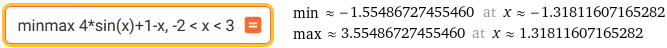
In modo simile posso trovare il massimo o il minimo di una funzione di più variabili.
Cerchiamo ad esempio il minimo di
function F(x,y) {return x+8*y+1/(x*y) }
a=0; b=5; c=0; d=5; h=b-a; k=d-c; min=1e100
for(i=0; i<4e8; i=i+1) {x=Math.random()*h+a, y=Math.random()*k+c
if(F(x,y) < min) { min=F(x,y); x1=x; y1=y } }
document.write("minimo = ",min," per x = ",x1," y = ",y1)
Output:
minimo = 6.000000017365355 per x = 1.9997906767795004 y = 0.2500076844477195
Ripeto per una conferma:
minimo = 6.000000131637009 per x = 2.0004354149325376 y = 0.2499292960503352
Output:
minimo = 6.000000017365355 per x = 1.9997906767795004 y = 0.2500076844477195
A questo punto posso restringere gli intervalli:
...
a=1.95; b=2.05; c=0.245; d=0.255; h=b-a; k=d-c
...
minimo = 6.000000000003121 per x = 2.0000004772980855 y = 0.2500002781931553
Posso assumere che il minimo sia 6 in (2,0.25).
Posso avere facilmente una conferma con WolframAlpha: min x+8y+1/(x*y) for x>0, y>0 6 at (x,y) = (2,1/4)
Un altro esempio: una tabella (T[C][R]) di 10 righe e 20 colonne, realizzata con una variabile indiciata a 10 posti avente come elementi variabili indiciate a 20 posti.
m = 10; n = 20
T = new Array(m); for(i=1; i <= n; i=i+1) {T[i] = new Array(n)}
for(R=1; R <= m; R=R+1) { for(C=1; C <= n; C=C+1)
{if(R==1|R==m|C==1|C==n) {x="0"} else {x="8"}; T[C][R]=x} }
// Ho messo i valori nella tabella. Ora la stampo:
for(R=1; R <= m; R=R+1) { for(C=1; C <= n; C=C+1)
{document.write( T[C][R]) }; document.write("<br>") }
o
m = 10; n = 20
T = new Array(m); for(i=1; i <= n; i=i+1) {T[i] = new Array(n)}
for(R=1; R <= m; R=R+1) { for(C=1; C <= n; C=C+1)
{if(R==1|R==m|C==1|C==n) {x="0"} else {x="8"}; T[C][R]=x} }
// Ho messo i valori nella tabella. Ora la stampo:
for(R=1; R <= m; R=R+1) {s=""; for(C=1; C <= n; C=C+1)
{s=s+" "+T[C][R]}; document.write(s) }
Output:
00000000000000000000
08888888888888888880
08888888888888888880
08888888888888888880
08888888888888888880
08888888888888888880
08888888888888888880
08888888888888888880
08888888888888888880
00000000000000000000
Come quasi tutto il software, JavaScript esegue i calcoli non in base dieci ma in base 2. Ad esempio 8
"internamente" è rappresentato come 1000 (1*2^3+0*2^2+0*2^1+0*1 = 8+0+0+0), 15 come 1111 (8+4+2+1), 0.25 come 0.01 (0*1+0*1/2+0*1/4 = 0+0+1/4),
0.125 come 0.001 (0+0+0+1/8).
Non tutti i numeri frazionari sono rappresentati esattamente. Ad esempio 0.3 non posso ottenerlo
come somma di un numero finito di mezzi, quarti, ottavi, ...; in base 2 diventa 0.010011001100110011...
Per questo motivo quando vengono eseguti i calcoli possono verificarsi errori di arrotondamento apparentemnte incomprensibili.
Ad esempio può capitare che mentre si attende come risultato di un certo programma 4.26 si ottenga invece 4.26000002 o 4.25999997.
In casi come questo, volendo, si può ricorrere al comando toFixed(n) che arrotonda il numero a n
cifre dopo il "." e lo memorizza sotto forma di stringa; col comando Number lo si riottiene in fomato numerico. Un esempio:
document.write( 1/10+1/5 ) ha come output 0.30000000000000004; usando ad esempio
x=1/10+1/5; document.write( x.toFixed(10) )
ottengo la stringa 0.3000000000; con
x=1/10+1/5; document.write( Number(x.toFixed(10)) )
ottengo il numero 0.3.
Un altro esempio:
x=3/10+3/5; y=x.toFixed(6); z=Number(y); document.write( x," ",y," ", z)
fornisce 0.8999999999999999 0.900000 0.9
Il calcolo degli integrali:
function F(x) { return Math.floor(x) }; a = 0; b = 5
document.write("F(x) = Math.floor(x); a = 0; b = 5<br>")
n=4321
for(i = 0; i < 5; i = i+1) {
s=0; h=(b-a)/n; for (var j=0; j < n; j=j+1) {s = s + F(a+(j+1/2)*h)}
document.writeln(n, " rettangoli, integrale su [a,b] di F = ", s*h, "<br>"); n=n*2 }
o
function F(x) { return Math.floor(x) }; a = 0; b = 5
document.write("F(x) = Math.floor(x); a = 0; b = 5")
n=4321
for(i = 0; i < 5; i = i+1) {
s=0; h=(b-a)/n; for (var j=0; j < n; j=j+1) {s = s + F(a+(j+1/2)*h)}
document.write(n, " rettangoli, integrale su [a,b] di F = ", s*h); n=n*2 }
Output:
F(x) = Math.floor(x); a = 0; b = 5
4321 rettangoli, integrale su [a,b] di F = 10
8642 rettangoli, integrale su [a,b] di F = 10
17284 rettangoli, integrale su [a,b] di F = 10
34568 rettangoli, integrale su [a,b] di F = 10
69136 rettangoli, integrale su [a,b] di F = 10
function F(x) { return Math.abs(x*(x-2)) }; a = 0; b = 3
document.write("F(x) = abs(x*(x-2)); a = 0; b = 3<br>")
n=4321
for(i = 0; i < 5; i = i+1) {
s=0; h=(b-a)/n; for (var j=0; j < n; j=j+1) {s = s + F(a+(j+1/2)*h)}
document.writeln(n, " rettangoli, integrale su [a,b] di F = ", s*h, "<br>"); n=n*2 }
o
function F(x) { return Math.abs(x*(x-2)) }; a = 0; b = 3
document.write("F(x) = abs(x*(x-2)); a = 0; b = 3")
n=4321
for(i = 0; i < 5; i = i+1) {
s=0; h=(b-a)/n; for (var j=0; j < n; j=j+1) {s = s + F(a+(j+1/2)*h)}
document.write(n, " rettangoli, integrale su [a,b] di F = ", s*h); n=n*2 }
Output:
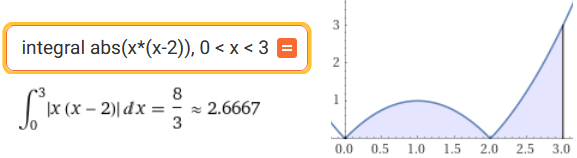
F(x) = abs(x*(x-2)); a = 0; b = 3
4321 rettangoli, integrale su [a,b] di F = 2.666666599728399
8642 rettangoli, integrale su [a,b] di F = 2.6666666499282217
17284 rettangoli, integrale su [a,b] di F = 2.666666662482534
34568 rettangoli, integrale su [a,b] di F = 2.6666666656205797
69136 rettangoli, integrale su [a,b] di F = 2.6666666664051637
Con WolframAlpha:
Un programma più sofisticato, che consente di valutare la precisione delle uscite.
Calcoliamo l'integrale di √(1-x³) tra -1 e ³√(6/7)
function F(x) { return Math.sqrt(1-x*x*x) }; a = -1; b = Math.cbrt(6/7)
document.writeln("N.rettangoli -- Integrale su [a,b] -- Per quanto viene divisa la variazione <br>")
I=0; D=0; n=4321
for(i = 0; i < 15; i = i+1) {
s=0; h=(b-a)/n; for (var j=0; j < n; j=j+1) {s = s + F(a+(j+1/2)*h)}
D1=s*h-I; E=D/D1; D=D1
document.writeln(n, " -- ", s*h, " -- ", E, "<br>"); I=s*h; n=n*2 }
o
function F(x) { return Math.sqrt(1-x*x*x) }; a = -1; b = Math.cbrt(6/7)
document.write("N.rettangoli -- Integrale su [a,b] -- Per quanto viene divisa la variazione")
I=0; D=0; n=4321
for(i = 0; i < 15; i = i+1) {
s=0; h=(b-a)/n; for (var j=0; j < n; j=j+1) {s = s + F(a+(j+1/2)*h)}
D1=s*h-I; E=D/D1; D=D1
document.write(n, " -- ", s*h, " -- ", E); I=s*h; n=n*2 }
N.rettangoli -- Integrale su [a,b] -- Per quanto viene divisa la variazione
4321 -- 1.9400079753541681 -- 0
8642 -- 1.9400079593151842 -- -120955790.2906261
17284 -- 1.9400079553054201 -- 3.999981947431363
34568 -- 1.9400079543029924 -- 4.000053161644848
69136 -- 1.9400079540523478 -- 3.9993984778566323
138272 -- 1.9400079539897481 -- 4.003926590144862
276544 -- 1.940007953974047 -- 3.9869329109627785
553088 -- 1.9400079539701467 -- 4.025732991744947
1106176 -- 1.940007953969082 -- 3.6631908237747655
2212352 -- 1.9400079539689208 -- 6.604683195592287
4424704 -- 1.9400079539688604 -- 2.6691176470588234
8849408 -- 1.9400079539689707 -- -0.5472837022132797
17698816 -- 1.9400079539687647 -- -0.5355603448275862
35397632 -- 1.9400079539690398 -- -0.7489911218724778
70795264 -- 1.9400079539685908 -- -0.612759643916914
Si vede che la variazione tra un'uscita e l'altra tende a ridursi, in corrispondenza del fatto che il programma converge verso il valore esatto (in questo caso la variazione tende a dividersi per 4). Ma ad un certo punto cambia la velocità con cui si riduce la variazione, che cambia anche segno. Mi fermo alle uscite 1.940007953969082, 1.9400079539689208, 1.9400079539688604 e prendo il valore 1.9400079539688 (il valore esatto proseguirebbe così: 1.94000795396883927287…)
Con WolframAlpha:

|
Si possono integrare in un unico file più programmi. Vediamo come mettere insieme quello per trovare la soluzione
di un'equazione e quello per il calcolo degli integrali in modo da determinare l'area della figura rappresentata a fianco:
la superficie che sta nel primo quadrante ed è racchiusa tra le curve y = 1/x e y = -x²+3 [trovo dove si azzera -x²+3 - 1/x tra 0 ed 1 e tra 1 e 2 e calcolo l'integrale di -x²+3-1/x tra i punti così trovati] | 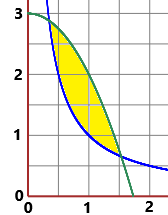 |
document.write ("le ascisse delle intersezioni:<br>")
function F(x) {return -x*x+3-1/x }
a=0; b=1
if(F(a)*F(b)>0) document.write ("F(a) e F(b) hanno segno =")
else {
for(i=0; i<100; i=i+1) {
m = a+(b-a)/2; y1 = F(a); y2 = F(m); y3 = F(b)
if(y1*y2 > 0) {a = m} else {b = m} }
document.write(m," ")
}
a=1; b=2; h=m
if(F(a)*F(b)>0) document.write ("F(a) e F(b) hanno segno =")
else {
for(i=0; i<100; i=i+1) {
m = a+(b-a)/2; y1 = F(a); y2 = F(m); y3 = F(b)
if(y1*y2 > 0) {a = m} else {b = m} }
document.write(m,"<br>")
}
n=4321; a=h; b=m
for(i = 0; i < 10; i = i+1) {
s=0; h=(b-a)/n; for (var j=0; j < n; j=j+1) {s = s + F(a+(j+1/2)*h)}
document.writeln(n, " rettangoli, integrale su [a,b] di F = ", s*h, "<br>"); n=n*2 }
o
document.write("le ascisse delle intersezioni:")
function F(x) {return -x*x+3-1/x }
a=0; b=1
if(F(a)*F(b)>0) document.write ("F(a) e F(b) hanno segno =")
else {
for(i=0; i<100; i=i+1) {
m = a+(b-a)/2; y1 = F(a); y2 = F(m); y3 = F(b)
if(y1*y2 > 0) {a = m} else {b = m} }
document.write(m)
}
a=1; b=2; h=m
if(F(a)*F(b)>0) document.write ("F(a) e F(b) hanno segno =")
else {
for(i=0; i<100; i=i+1) {
m = a+(b-a)/2; y1 = F(a); y2 = F(m); y3 = F(b)
if(y1*y2 > 0) {a = m} else {b = m} }
document.write(m)
}
n=4321; a=h; b=m
for(i = 0; i < 10; i = i+1) {
s=0; h=(b-a)/n; for (j=0; j < n; j=j+1) {s = s + F(a+(j+1/2)*h)}
document.write(n, " rettangoli, integrale su [a,b] di F = ", s*h); n=n*2 }
Output:
le ascisse delle intersezioni:
0.3472963553338606 1.5320888862379562
4321 rettangoli, integrale su [a,b] di F = 0.8853761909207116
8642 rettangoli, integrale su [a,b] di F = 0.8853761668754514
...
1106176 rettangoli, integrale su [a,b] di F = 0.8853761588608665
2212352 rettangoli, integrale su [a,b] di F = 0.885376158860398
L'area (arrotondata) è 0.885376158860 (poco meno di un quadrato di lato 1).
È comodissimo (e più affidabile di certe formulette suggerite da molti manuali di fisica) ricorrere a semplifici
programmini per calcolare il valore approssimato di una grandezza funzione di altre note con una certa precisione.
Si ricorre alla funzione random() (che assume un valore a caso con distribuzione uniforme tra 0 ed 1) per generare moltissimi valori
delle grandezze "note" e, poi, prendere il minimo e il massimo valore assunto dalla funzione.
Un primo esempio.
So che y = x*sin(x³) con x = 2 +/- 0.05. Quanto vale y?
// x*sin(x^3) con x = 2 +/- 0.05
min=1e100; max=-1e100; a=2; eps=0.05
for(i=1; i<1e6; i=i+1)
{x = a + eps*(Math.random()*2-1)
y = x*Math.sin(Math.pow(x,3))
if(y < min) min=y; if(y > max) max=y }
document.write("min=",min," max=",max,"<br>")
document.write(min+(max-min)/2," +/- ", (max-min)/2)
o senza "<br>"
min=1.4842996222416736 max=1.9895379331258574
1.7369187776837656 +/- 0.2526191554420919
Concludo che y = 1.737 ± 0.253, o che y = 1.74 ± 0.26
| Altro esempio. Nel caso illustrato a fianco ? = g*m*sin(a°) dove g = 9.80±0.02, m = 0.3±0.006, a =30 ± 1. Quanto vale ? e con che precisione?
// g*m*sin(a*pi/180)
min=1e100; max=-1e100
g=9.8; eg=0.02; m=0.3; em=0.006; a=30; ea=1
for(i=1; i<1e8; i=i+1)
{g1=g+eg*(Math.random()*2-1)
m1=m+em*(Math.random()*2-1)
a1=a+ea*(Math.random()*2-1)
f = g1*m1*Math.sin(a1*Math.PI/180)
if(f < min) min=f; if(f > max) max=f }
document.write("min=",min," max=",max,"<br>")
document.write(min+(max-min)/2," +/- ", (max-min)/2)
o senza "<br>"
min=1.394086324166626 max=1.5475206560099448
1.4708034900882854 +/- 0.07671716592165945 | 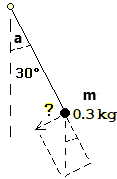 |
Concludo che ? = 1.471 ± 0.077, o 1.47 ± 0.08 (valore in Newton, pari a circa 0.150±0.008 kg)
Per evitare di mettere "Math." di fronte alle funzioni matematiche si può racchiudere il programma tra
Esempio: In un partita a dadi i giocatori lanciano tre dadi; vince chi per primo ottiene almeno 2 numeri uguali. Qual è la probabilità di ottenere ciò in un solo lancio?
["floor" è la parte intera, "random" genera un numero casuale compreso tra 0 ed 1]
with (Math) {
n=1e4; x=0; for(i=0; i<n; i=i+1)
{ U1=floor(random()*6+1); U2=floor(random()*6+1); U3=floor(random()*6+1); s=0
if(U1==U2) s=1; if(U1==U3) s=1; if(U2==U3) s=1; x=x+s}
document.writeln("n=",n," P = ",x/n*100,"% +/- ",sqrt(x/n*(1-x/n)/sqrt(n-1)*300),"%<br>" )
n=n*10; x=0; for(i=0; i<n; i=i+1)
{ U1=floor(random()*6+1); U2=floor(random()*6+1); U3=floor(random()*6+1); s=0
if(U1==U2) s=1; if(U1==U3) s=1; if(U2==U3) s=1; x=x+s}
document.write("n=",n," P = ",x/n*100,"% +/- ",sqrt(x/n*(1-x/n)/sqrt(n-1)*300),"%<br>" )
n=n*10; x=0; for(i=0; i<n; i=i+1)
{ U1=floor(random()*6+1); U2=floor(random()*6+1); U3=floor(random()*6+1); s=0
if(U1==U2) s=1; if(U1==U3) s=1; if(U2==U3) s=1; x=x+s}
document.writeln("n=",n," P = ",x/n*100,"% +/- ",sqrt(x/n*(1-x/n)/sqrt(n-1)*300),"%<br>" )
}
o
with(Math) {
n=1e4; x=0; for(i=0; i<n; i=i+1)
{ U1=floor(random()*6+1); U2=floor(random()*6+1); U3=floor(random()*6+1); s=0
if(U1==U2) s=1; if(U1==U3) s=1; if(U2==U3) s=1; x=x+s}
document.write("n=",n," P = ",x/n*100,"% +/- ",sqrt(x/n*(1-x/n)/sqrt(n-1)*300),"%" )
n=n*10; x=0; for(i=0; i<n; i=i+1)
{ U1=floor(random()*6+1); U2=floor(random()*6+1); U3=floor(random()*6+1); s=0
if(U1==U2) s=1; if(U1==U3) s=1; if(U2==U3) s=1; x=x+s}
document.write("n=",n," P = ",x/n*100,"% +/- ",sqrt(x/n*(1-x/n)/sqrt(n-1)*300),"%" )
n=n*10; x=0; for(i=0; i<n; i=i+1)
{ U1=floor(random()*6+1); U2=floor(random()*6+1); U3=floor(random()*6+1); s=0
if(U1==U2) s=1; if(U1==U3) s=1; if(U2==U3) s=1; x=x+s}
document.write("n=",n," P = ",x/n*100,"% +/- ",sqrt(x/n*(1-x/n)/sqrt(n-1)*300),"%" )
}
Output:
n=10000 P = 44.45% +/- 0.8606952368524986%
n=100000 P = 44.423% +/- 0.483964164681482%
n=1000000 P = 44.4386% +/- 0.2721620141336594%
La precisione calcolata da sqrt(x/n*(1-x/n)/sqrt(n-1)*3 (il valore messo dopo "+/-") non è "certa": c'è una
piccolissima probabilità (0.03%) che lo scarto del valore trovato dal valore vero sia maggiore di essa
[se prendo
Posso concludere che la probabilità è 44.4% ± 0.3.
Aumentando il numero delle prove, impiegando più
tempo, potrei ottenere valutazioni migliori (ad esempio con
n=100000000 posso ottenere P=44.443728% ± 0.08606615804962461% o valori simili, ovvero 44.444% ± 0.090%). Ma ce n'è d'avanzo delle uscite precedenti per rispondere al quesito (si può congetturare che la risposta
sia 44.444…% = 4/9; ed è proprio così; prova a trovarne una dimostrazione).
Altro problema: Nella popolazione di adulti in una determinata regione una particolare malattia infantile colpisce 1 persona su 8. Considera 100 persone adulte di quella regione, calcola la probabilità che non più di 10 ne siano state colpite.
with(Math) {
P = 1/8
n=1e4; x=0; for(i=0; i<n; i=i+1) { k=0; for(j=0; j<100; j=j+1) if(random() < P) k=k+1; if(k<11) x=x+1 }
document.write (x/n*100,"% +/- ",sqrt(x/n*(1-x/n)/sqrt(n-1)*300),"%<br>" )
n=n*2; x=0; for(i=0; i<n; i=i+1) { k=0; for(j=0; j<100; j=j+1) if(random() < P) k=k+1; if(k<11) x=x+1 }
document.write (x/n*100,"% +/- ",sqrt(x/n*(1-x/n)/sqrt(n-1)*300),"%<br>" )
n=n*2; x=0; for(i=0; i<n; i=i+1) { k=0; for(j=0; j<100; j=j+1) if(random() < P) k=k+1; if(k<11) x=x+1 }
document.write (x/n*100,"% +/- ",sqrt(x/n*(1-x/n)/sqrt(n-1)*300),"%<br>" )
n=n*2; x=0; for(i=0; i<n; i=i+1) { k=0; for(j=0; j<100; j=j+1) if(random() < P) k=k+1; if(k<11) x=x+1 }
document.write (x/n*100,"% +/- ",sqrt(x/n*(1-x/n)/sqrt(n-1)*300),"%<br>" )
n=n*2; x=0; for(i=0; i<n; i=i+1) { k=0; for(j=0; j<100; j=j+1) if(random() < P) k=k+1; if(k<11) x=x+1 }
document.write (x/n*100,"% +/- ",sqrt(x/n*(1-x/n)/sqrt(n-1)*300),"%<br>" )
}
o
with(Math) {
P = 1/8
n=1e4; x=0; for(i=0; i<n; i=i+1) { k=0; for(j=0; j<100; j=j+1) if(random() < P) k=k+1; if(k<11) x=x+1 }
document.write(x/n*100,"% +/- ",sqrt(x/n*(1-x/n)/sqrt(n-1)*300),"%")
n=n*2; x=0; for(i=0; i<n; i=i+1) { k=0; for(j=0; j<100; j=j+1) if(random() < P) k=k+1; if(k<11) x=x+1 }
document.write(x/n*100,"% +/- ",sqrt(x/n*(1-x/n)/sqrt(n-1)*300),"%")
n=n*2; x=0; for(i=0; i<n; i=i+1) { k=0; for(j=0; j<100; j=j+1) if(random() < P) k=k+1; if(k<11) x=x+1 }
document.write(x/n*100,"% +/- ",sqrt(x/n*(1-x/n)/sqrt(n-1)*300),"%")
n=n*2; x=0; for(i=0; i<n; i=i+1) { k=0; for(j=0; j<100; j=j+1) if(random() < P) k=k+1; if(k<11) x=x+1 }
document.write(x/n*100,"% +/- ",sqrt(x/n*(1-x/n)/sqrt(n-1)*300),"%")
n=n*2; x=0; for(i=0; i<n; i=i+1) { k=0; for(j=0; j<100; j=j+1) if(random() < P) k=k+1; if(k<11) x=x+1 }
document.write(x/n*100,"% +/- ",sqrt(x/n*(1-x/n)/sqrt(n-1)*300),"%")
}
Output:
27.27% +/- 0.7713843934368594%
27.98% +/- 0.6538211585784399%
28.15% +/- 0.5508088755674877%
28.01375% +/- 0.46248738076123164%
27.995% +/- 0.3888238297425278%
Cerca di capire come è impostato il programma.
Posso concludere che la probabilità (arrotondata) è 28%.
Un altro: Lancio una moneta equilibrata 200 volte. Qual è la probabilità di ottenere 100 testa?
with(Math) {
n=1e4; x=0; for(i=0; i<n; i=i+1) { Head=0; for(j=0; j<200; j=j+1) if(random() > 0.5) Head=Head+1; if(Head==100) x=x+1 }
document.write(x/n*100,"% +/- ",sqrt(x/n*(1-x/n)/sqrt(n-1)*300),"%<br>" )
n=n*2; x=0; for(i=0; i<n; i=i+1) { Head=0; for(j=0; j<200; j=j+1) if(random() > 0.5) Head=Head+1; if(Head==100) x=x+1 }
document.write(x/n*100,"% +/- ",sqrt(x/n*(1-x/n)/sqrt(n-1)*300),"%<br>" )
n=n*2; x=0; for(i=0; i<n; i=i+1) { Head=0; for(j=0; j<200; j=j+1) if(random() > 0.5) Head=Head+1; if(Head==100) x=x+1 }
document.write(x/n*100,"% +/- ",sqrt(x/n*(1-x/n)/sqrt(n-1)*300),"%<br>" )
n=n*2; x=0; for(i=0; i<n; i=i+1) { Head=0; for(j=0; j<200; j=j+1) if(random() > 0.5) Head=Head+1; if(Head==100) x=x+1 }
document.write(x/n*100,"% +/- ",sqrt(x/n*(1-x/n)/sqrt(n-1)*300),"%<br>" )
n=n*2; x=0; for(i=0; i<n; i=i+1) { Head=0; for(j=0; j<200; j=j+1) if(random() > 0.5) Head=Head+1; if(Head==100) x=x+1 }
document.write(x/n*100,"% +/- ",sqrt(x/n*(1-x/n)/sqrt(n-1)*300),"%<br>" )
n=n*2; x=0; for(i=0; i<n; i=i+1) { Head=0; for(j=0; j<200; j=j+1) if(random() > 0.5) Head=Head+1; if(Head==100) x=x+1 }
document.write(x/n*100,"% +/- ",sqrt(x/n*(1-x/n)/sqrt(n-1)*300),"%<br>" )
}
o senza "<br>"
Output:
5.93% +/- 0.4090952189333392%
5.635% +/- 0.33586209262412553%
5.4425% +/- 0.27784050102591434%
5.65625% +/- 0.23790871617461437%
5.595% +/- 0.19903472541622463%
La probabilità è 5.6% (± 0.2%).
La lunghezza di un arco di curva (calcolando la lunghezza della spezzata che approssima la curva). Un esempio: la lunghezza del grafico della funzione x → x³-2x tra il punto di ascissa -1.5 e quello di ascissa 1.5.
a=-1.5; b=1.5
document.write("la lunghezza della curva da t=a e t=b<br>")
function x(t) {return t}; function y(t) {return t*t*t-2*t}
n = 1e6; e=(b-a)/n; L=0
for(i=1;i<=n; i=i+1) {t1=a+(i-1)*e; t2=a+i*e
L = L+ Math.sqrt(Math.pow(x(t1)-x(t2),2)+Math.pow(y(t1)-y(t2),2))}
document.write("n = "+n+" L = "+L+"<br>")
n = n*2; e=(b-a)/n; L=0
for(i=1;i<=n; i=i+1) {t1=a+(i-1)*e; t2=a+i*e
L = L+ Math.sqrt(Math.pow(x(t1)-x(t2),2)+Math.pow(y(t1)-y(t2),2))}
document.write("n = "+n+" L = "+L+"<br>")
n = n*2; e=(b-a)/n; L=0
for(i=1;i<=n; i=i+1) {t1=a+(i-1)*e; t2=a+i*e
L = L+ Math.sqrt(Math.pow(x(t1)-x(t2),2)+Math.pow(y(t1)-y(t2),2))}
document.write("n = "+n+" L = "+L+"<br>")
o senza <br> e +"<br>"
Output:
la lunghezza della curva da t=a e t=b
n = 1000000 L = 6.179914900645402
n = 2000000 L = 6.179914900650324
n = 4000000 L = 6.1799149006518075
Se mi fermo qui, prendo L = 6.1799149007
Altro esempio: la lunghezza dell'ellisse di semiassi 2 e 1.
a=0; b=2*Math.PI
...
function x(t) {return 2*Math.cos(t)}; function y(t) {return Math.sin(t)}
...
n = 1000000 L = 9.68844822053149
n = 2000000 L = 9.68844822054401
n = 4000000 L = 9.688448220546611
n = 8000000 L = 9.688448220547578
L = 9.688448220548
La distanza di una curva da un punto. Un esempio: l'ellisse x=2+2*cos(t), y=-1+5*sin(t) da (10,10). Vedi l'immagine seguente, a sinistra.
a=0; b=2*Math.PI; xP=10; yP=10
document.write("il punto Q piu' vicino, la distanza, e il parametro t<br>")
function x(t) {return 2+2*Math.cos(t)}; function y(t) {return -1+5*Math.sin(t)}
d=Math.pow(10,300)
n = 1e6; e=(b-a)/n
for(i=0;i<=n; i=i+1) {t=a+i*e
d1 = Math.pow(xP-x(t),2)+Math.pow(yP-y(t),2); if(d1<d) {d=d1; t0=t} }
document.write("t = "+t0+" d = "+Math.sqrt(d)+" Q = ("+x(t0)+","+y(t0)+")<br>")
n = n*2; e=(b-a)/n
for(i=0;i<=n; i=i+1) {t=a+i*e
d1 = Math.pow(xP-x(t),2)+Math.pow(yP-y(t),2); if(d1<d) {d=d1; t0=t} }
document.write("t = "+t0+" d = "+Math.sqrt(d)+" Q = ("+x(t0)+","+y(t0)+")<br>")
o senza <br>
Output:
il punto Q piu' vicino, la distanza, e il parametro t
t = 1.1507653890099412 d = 9.644700186961918 Q = (2.815577403627406,3.565381623350601)
t = 1.1507653890099412 d = 9.644700186961918 Q = (2.815577403627406,3.565381623350601)
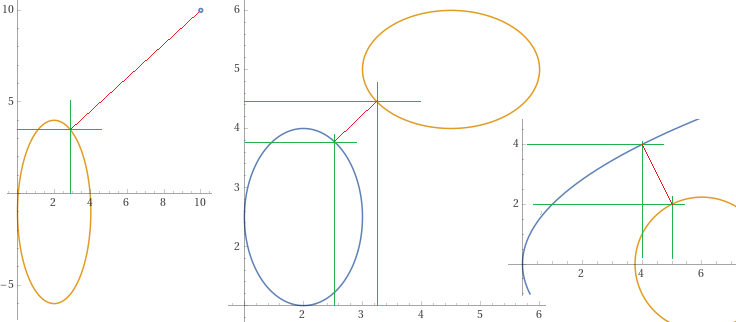
La distanza tra due curve, generando punti casuali e trovando quelli con minima distanza. Un esempio: le ellissi x=cos(t)+2, y=-1.5*sin(t)+2.5 e x=1.5*cos(t)+4.5, y=sin(t)+5. Vedi l'immagine al centro. Per capire quante cifre prendere puoi ripetere un'altra volta il calcolo, eventualmente generando più punti o restringendo gli intervalli in cui far variare le x e le y.
a1=0; b1=2*Math.PI; a2=0; b2=2*Math.PI
document.write("i punti Q1, Q2 piu' vicini, la distanza (arrotonda a 4 o 5 cifre)<br>")
function x1(t) {return Math.cos(t)+2}; function y1(t) {return -Math.sin(t)*1.5+2.5}
function x2(t) {return 1.5*Math.cos(t)+4.5}; function y2(t) {return Math.sin(t)+5}
d=Math.pow(10,300)
n = 1e8
for(i=0;i<=n; i=i+1) { j=Math.random()*(b1-a1)+a1; k=Math.random()*(b2-a2)+a2
d1=Math.pow(x1(j)-x2(k),2)+Math.pow(y1(j)-y2(k),2)
if(d1<d) {d=d1;u1=x1(j);v1=y1(j);u2=x2(k);v2=y2(k)} }
document.write("d = "+Math.sqrt(d)+"<br>")
document.write("Q1 = ("+u1+","+v1+") Q2 = ("+u2+","+v2+")<br>")
o senza <br>
Output:
i punti Q1, Q2 piu' vicini, la distanza (arrotonda a 4 o 5 cifre)
d = 0.9860242151803079
Q1 = (2.5546711154464536,3.748104521184472) Q2 = (3.2517262590871874,4.4454981543974075)
Prendo Q1 = (2.5547, 3.7481), Q2 = (3.2517, 4.4455), distanza = 0.986024
Con più prove o restringendo gli intervalli potrei avere
Q1 = (2.5547,3.7481), Q2 = (3.2519,4.4453), distanza = 0.98602415
Altro esempio: la parabola x = y² e il cerchio di centro (6,0) e raggio √5. Vedi l'immagine sopra a destra.
a1=0; b1=5; a2=Math.PI/2; b2=Math.PI
document.write("i punti Q1, Q2 piu' vicini, la distanza (arrotonda a 4 o 5 cifre)<br>")
function x1(t) {return t*t/4}; function y1(t) {return t}
function x2(t) {return Math.cos(t)*Math.sqrt(5)+6}; function y2(t) {return Math.sin(t)*Math.sqrt(5)}
d=Math.pow(10,300)
n = 1e8
for(i=0;i<=n; i=i+1) { j=Math.random()*(b1-a1)+a1; k=Math.random()*(b2-a2)+a2
d1=Math.pow(x1(j)-x2(k),2)+Math.pow(y1(j)-y2(k),2)
if(d1<d) {d=d1;u1=x1(j);v1=y1(j);u2=x2(k);v2=y2(k)} }
document.write("d = "+Math.sqrt(d)+"<br>")
document.write("Q1 = ("+u1+","+v1+") Q2 = ("+u2+","+v2+")<br>")
o senza <br>
Output:
i punti Q1, Q2 piu' vicini, la distanza (arrotonda a 4 o 5 cifre)
d = 2.236067984608475
Q1 = (3.9998387984062047,3.999919398391025) Q2 = (4.9998326891487785,1.9999163358262355)
Prendo Q1 = (4,4), Q2 = (5,2), distanza = 2.236068 (ci sono anche i simmetrici rispetto all'asse x)
Le figure sono state realizzate con WolframAlpha.
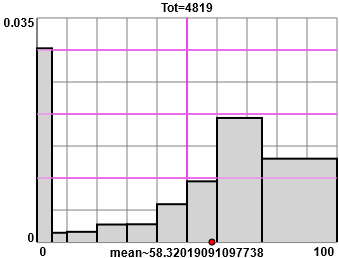
La programmazione consente di realizzare elaborazioni non fornite dai software più diffusi. Ad esempio è possibile realizzare istogrammi relativi a frequenze classificate in intervalli di diversa ampiezza. Un esempio: conoscendo le migliaia di persone morte in Italia nel 1951 negli intervalli di età [0,5),[5,10),[10,20),[20,30),[30,40),[40,50),[50,60),[60,75),[75,100) come rappresentare le frequenze percentuali unitarie (o densità) con uno script (sono modificabili i dati senza dover comprendere i comandi presenti nel programma): vedi qui come ottenere l'istogramma a sinistra.
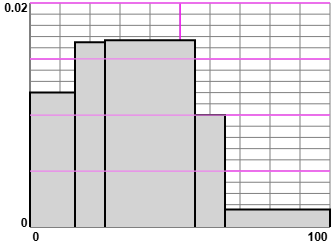
In una certa città, nel 1970, gli abitanti con meno di 15 anni sono il 18%, quelli con almeno 15 anni e meno di 25 sono il 16.5%, quelli con almeno 25 anni e meno di 55 sono il 50%, quelli con almeno 55 e meno di 65 sono il 10%, quelli con almeno 65 sono il 5.5%. Vedi qui come ottenere l'istogramma a destra.
Grafici di questo tipo possono essere ottenuti anche con questi
script.
abs(a) / |a| log10(a) / log of a base 10
acos(a) / arc cosine of a max(a,b)
asin(a) / arc sine of a min(a,b)
atan(a) / arc tangent of a pow(a,b) / a to the power b
atan2(a,b) / arc tangent of a/b random() / random n. in [0,1)
cbrt(a) / cube root of a round(a) / integer closest to a
ceil(a) / integer closest to a not < a sign(a) / sign of a
cos(a) / cosine of a sin(a) / sine of a
exp(a) / exponential of a sqrt(a) / square root of a
floor(a) / integer closest to a not > a tan(a) / tangent of a
log(a) / log of a base e trunc(a) / integer portion of a
log2(a) / log of a base 2 PI / π
cosh(a),sinh(a),tanh(a), acosh(a),asinh(a),atanh(a) hyperbolic functions
Note: M%N is the remainder of M/N, != is "not equal"
|