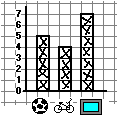L'utilizzo delle risorse informatiche nelle varie discipline
utilizzando software online
Carlo Dapueto - ALIMA - 30/10/2023
01 Questo incontro è successivo a quello condotto dal prof. Lorenzo Repetto, "Problemi, soluzioni,
codifiche", in cui è stata fatta una rassegna storica dell'informatica e sono stati illustrati esempi d'uso di molti
software impiegabili nei vari livelli scolastici, e a quello svoltosi in aula computer.
I materiali relativi a questi due incontri sono reperibili qui. Nel corso di questa presentazione si terrà conto delle risposte al questionario ivi riportato.
02 La programmazione (ovvero il "coding" - computer programming or coding) nella scuola preuniversitaria (tranne che nelle scuole superiori ad indirizzo scientifico-informatico), non deve essere una disciplina specifica del percorso formativo ma deve essere oggetto di un duplice tipo di attività. Da una parte deve fornire agli alunni un'idea concreta di cosa vuol dire mettere a punto un algoritmo e di come sia possibile tradurlo in modo che sia eseguibile da un computer (o un cellulare), dall'altra introdurre nell'insegnamento, sin dalla scuola di base, e in tutte le discipline, non solo in matematica, l'utilizzo consapevole di risorse informatiche per modellizzare e studiare gli aspetti della realtà con gli strumenti disciplinari.
03 La programmazione consiste nel tradurre un algoritmo (cioè
un procedimento costituito da una sequenza di "passi" atto a raggiungere un certo "risultato") in una sequenza di istruzioni scritte in un linguaggio simbolico che un computer sia in grado di tradurre in azioni meccaniche di vario tipo. I primi algoritmi di cui siamo a conoscenza sono quelli messi a punto dagli antichi Babilonesi, che tra l'altro, 4000 anni fa, avevano già acquisito l'idea di numero illimitato (ora diremmo il concetto di "numero reale"), sviluppato una tecnica per calcolare le radici quadrate, … (concetti e abilità poi perse da Greci e Romani); vedi (idee perse anche da gran parte della scuola italiana: vedi).
04 Tra i primi algoritmi
che apprendono gli alunni vi sono quelli per eseguire le operazioni, algoritmi che devono essere semplici e comprensibili, in grado di essere richiamati alla memoria facilmente (per l'esecuzione veloce si dovrà educare, sin dalla scuola di base, all'uso, consapevole, di calcolatrici e telefonini). Appresi, operativamente, gli algoritmi (che non devono essere a "percorso unico" e che devono variare a seconda dell'ordine di grandezza dei numeri coinvolti e della situazione oggetto del calcolo) un utile esercizio è far esplicitare a parole la strategia impiegata. Esempio:
Prova a spiegare come è stata eseguita la divisione illustrata a fianco. | |  |
05 Un altro esempio, che coinvolge
la lingua italiana: Cliccando qui
potete vedere delle immagini che illustrano come si fa il purè. È una delle ricette possibili: ne esistono altre leggermente
diverse. Provate a scrivere un elenco di frasi corrispondenti alle immagini che spieghino ad una persona (che non
abbia la possibilità di vedere queste immagini) come fare il purè. | |  |
|
È un tipico esercizio di lingua italiana, ma non solo, che consiste nella descrizione, mediante frasi numerate, di un procedimento da seguire. Il confronto tra le idee e le proposte degli alunni, gli opportuni interventi dell'insegnante, la discussione degli obiettivi comunicativi del testo che si sta realizzando, … danno a questa attività (e alle molte analoghe che si possono ideare) una valenza educativa notevole. La descrizione dei procedimenti (anche la descrizione delle ricette) è anche una delle prime attività di tipo "informatico" affrontabili a scuola.
|
06 Anche il gioco
offre occasioni (non etichettabili come disciplinari) di esplorazione, e visualizzazione, di algoritmi. QUI un esempio (come uscire dal Castello stregato).
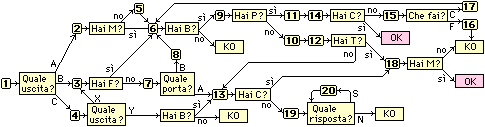
QUI le "soluzioni" | | 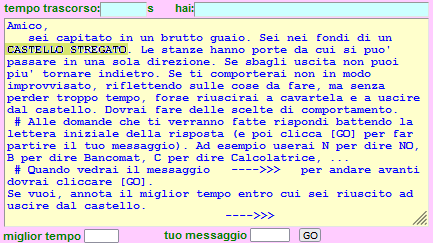 |
07 Uno dei primi algoritmi che gli alunni apprendono è quello
per mettere in ordine alfabetico delle parole (che poi servirà, indirettamente, anche per utilizzare i dizionari). Lo apprendono
operativamente, attraverso esempi e spiegazioni a parole dell'insegnante. Nelle scuola secondaria di 1º grado si potrà far esplicitare
l'algoritmo, arrivando a frasi del tipo:
(1) Se le due parole iniziano con lettere diverse metti quella con la lettera che appare per prima nell'alfabeto prima dell'altra parola; hai finito. Altrimenti confronta le lettere successive.
(2) Se una delle due parole non ha lettere successive metti questa parola prima dell'altra parola; hai finito.
(3) Se le lettere sono diverse metti la parola con la lettera che appare per prima nell'alfabeto prima dell'altra parola; hai finito. Altrimenti confronta le lettere successive.
(4) Vai al passo (2)
Sin dai primi anni di scuola di base si possono usare in rete dei semplici strumenti che consentono di ordinare parole o numeri. Due
esempi di script che gli alunni possono usare "da soli": UNO,
DUE.
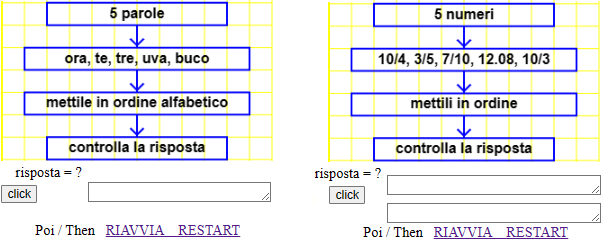
08 Questi script sono eseguiti direttamente in Internet.
Sono redatti in JavaScript, il linguaggio di programmazione incorporato nei browser e il linguaggio di programmazione di gran lunga più usato (lo usiamo per prenotare qualche servizio, per fare delle ricerche, …). Possiamo impiegarlo anche in modo semplice, per imparare, ad un primo livello, ad usare un linguaggio di programmazione universale.
Facciamo ricorso ad uno dei molti siti in cui si può programmare in JavaScript:
www.learnhindituts.com/online-javascript-compiler
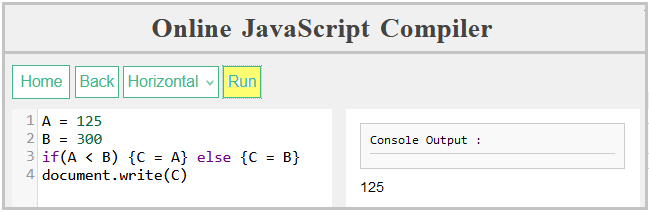
Che cosa producono i seguenti programmi? Cerca di capirlo e poi copia e incolla nella finestra sinistra ciascun programma e clicca Run.
A = 125
B = 300
if(A < B) {C = A} else {C = B}
document.write(C) | A = 125
B = 300/5
if(A < B) {C = A} else {C = B}
document.write(C) |
A = 'cassa'
B = 'casa'
if(A < B) {C = A} else {C = B}
document.write(C) | A = 'cara'
B = 'casa'
if(A < B) {C = A} else {C = B}
document.write(C) |
Questi sono esempi semplici, affrontabili anche nella scuola di base, non per imparare a programmare, ma per dare agli alunni
l'idea di come fa il computer (o il cellulare) a produrre certi risultati. Questo aspetto ("razionalizzare" i fenomeni) è importantissimo nell'insegnamento.
Nella scuola superiore di 2º grado, volendo, si possono implementare
algoritmi più complessi. Alcuni esempi si possono trovare qui.
09 Nella scuola secondaria si possono, oltre ad eseguire, anche esplorare
"internamente" degli script, come lo script divisori accessibile da qui
(proviamo a impiegarlo).

Il "codice sorgente" posso visualizzarlo con Ctrl+U ( -Option-U nei Mac), od anche usando il menu View/Visualizza o comandi simili del browser, come si può fare con tutti i documenti Html.
Per accedere direttamente al codice sorgente (ed eventualmente modificarlo) si può aprire il file con Blocco_Note o
un altro editor di testi. In questo caso devo aprire https://www.macosaweb.it/script/divisori.htm (devo mettere ciò nella casella
che si apre azionado il comando "Apri" o "Open" o …)
-Option-U nei Mac), od anche usando il menu View/Visualizza o comandi simili del browser, come si può fare con tutti i documenti Html.
Per accedere direttamente al codice sorgente (ed eventualmente modificarlo) si può aprire il file con Blocco_Note o
un altro editor di testi. In questo caso devo aprire https://www.macosaweb.it/script/divisori.htm (devo mettere ciò nella casella
che si apre azionado il comando "Apri" o "Open" o …)
<script>
function divisor() {
d=2; n = document.cal.n.value; document.cal.v.value = 1;
while (d < n) {q=n%d; if(q==0) {document.cal.v.value = document.cal.v.value+" "+d}; d=d+1};
// n % d e' il resto della divisione intera tra n e d
document.cal.v.value=document.cal.v.value+" "+n
}
</script>
<form name="cal">
numero intero positivo <input type="text" name="n" value="" size=9>
<input type="button" value="calcola i suoi divisori" onClick="divisor()"><br>
<textarea name="v" cols=70 rows=25></textarea>
</form>
Il programma vero e proprio è racchiuso tra <script> e </script> (in questo caso
contiene una sola "procedura", ossia un solo "sottoprogramma"; in JavaScript i sottoprogrammi sono chiamati "function").
while significa "fin tanto che". La parte che segue </script> definisce che cosa appare sullo schermo del computer;
il suo significato è abbastanza evidente.
Costruita un'idea di che cosa sia un programma, si potranno usare (non più "a scatola nera")
programmi più sofisticati (se accompagnati da un'attività didattica che ne faccia comprendere ruolo, potenzialità
e limiti).
10 Facciamo ora vari esempi di intreccio con le altre discipline.
Iniziamo dalle discipline linguistiche.
Ordinamento di parole con lo script ordina parole accessibile da qui.
Copiamo e incolliamo queste parole, clicchiamo "in ordine" e vediamo che cosa accade:
alice, cominciava, a, sentirsi, mortalmente, stanca, di, sedere, sul, poggio, accanto, a, sua, sorella, senza, far, nulla, a, che, serve, un, libro, penso', alice, senza, immagini, e, dialoghi

11 L'uso del software consente anche di esercitare, in un contesto operativo,
semplici usi delle lingue straniere. Un esempio, in un contesto informatico-linguistico (ricordiamo che code: a system of words, letters or symbols that you use instead of ordinary writing, so that the information can only be understood by someone else who know the system; figure: a number from 0 to 9, written as a character rather than a word).
Un esempio: lo script codifica
accessibile da qui
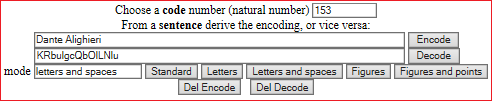
Che cosa ha introdotto una persona se dopo aver
scelto come chiave (key, numero che serve per decifrare la parola codificata) 123, aver selezionato "Figures and points" ha ottenuto
come codifica 9628.48829? Ovvero, qual è la decodifica di 9628.48829?
Gli algoritmi (e la matematica) sono presenti in una marea di circostanze della vita quotidiana. La scuola fa riflettere su questo aspetto?
12 Vediamo come usare, in contesti linguistici,
WolframAlpha, il software matematico libero più diffuso al mondo.

Vediamo cosa si ottiene mettendo in WolframAlpha
translate figure from English to Italian
Vediamo cosa si ottiene mettendo in WolframAlpha
number name 12345.6789
Vediamo cosa si ottiene mettendo in WolframAlpha
compare italiano, english
Vediamo cosa si ottiene mettendo in WolframAlpha
sort("alice", "cominciava", "a", "sentirsi", "mortalmente", "stanca", "di", "sedere", "sul", "poggio", "accanto", "a", "sua", "sorella", "senza", "far", "nulla")
[non posso mettere anche "a",..., "dialoghi" in quanto ci sono dei limiti a cosa introdurre come input]
13 Continuiamo a vedere con WolframAlpha come
si può esplorare la matematica che interviene nelle discipline artistico-figurative.
Vediamo cosa si ottiene mettendo in WolframAlpha
vanishing points
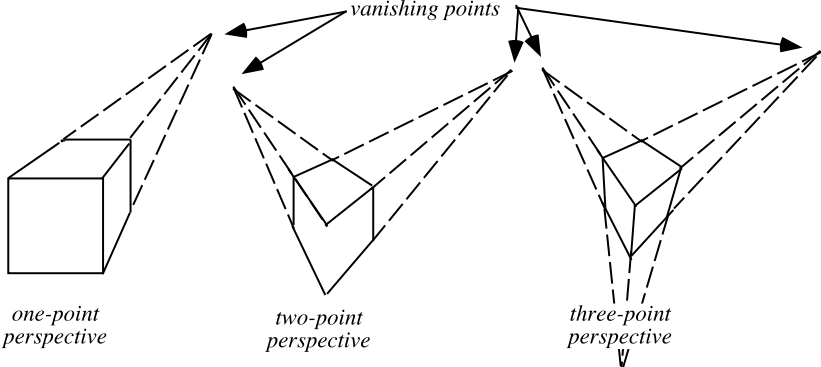
I "vanishing points" sono i punti di fuga. Sopra ne sono visualizzati tre ma, ovviamente,
possono essere molti di più.
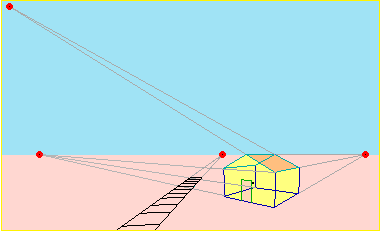
Vediamo un cubo (centrato in (0,0,0) con lati lunghi 1 e paralleli agli assi)
da diversi punti di vista.
Se metto in WolframAlpha cube view from (2,1,1)
ottengo la figura a destra. Che cosa ottengo con i seguenti input?
cube view from (2,2,2)
cube view from (1000,1000,1000)
cube view from (0,2,2) | | 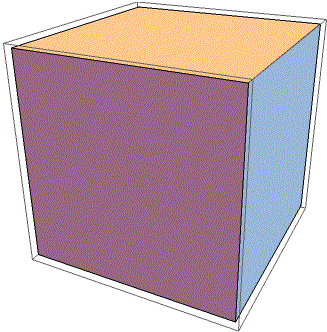 |
14 Dopo alcune anticipazioni di Brunelleschi e Leon Battista Alberti, fu
Piero della Francesca a fare una trattazione rigorosa della prospettiva, con il De prospectiva pingendi (~1474).
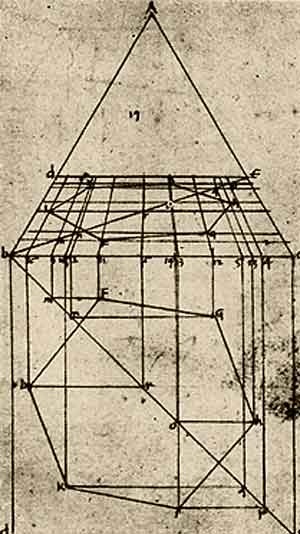

Le sue spiegazioni non hanno come soggetti esempi pittorici, ma sono argomentazioni e descrizioni di procedimenti di costruzione geometrica generali, che chiama "teoremi". La figura a sinistra è una delle molte presenti nel suo trattato (a destra la sua "Flagellazione", 1460).
Possiamo dire che questo "artista" ha scritto la prima opera matematica sulla geometria proiettiva.
| Cliccando QUI si
accede a un file che consente di realizzare le immagini descritte nella animazione rappresentata a lato.
Un semplice esempio di come, con l'aiuto del computer, si può facilmente esplorare questo tema. |
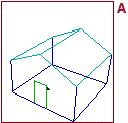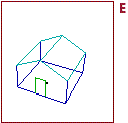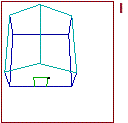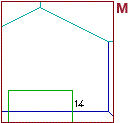 |
|
[l'immagine a destra è un gif animato, ottenuto concatenando più immagini: altro aspetto del ruolo dell'informatica] |
Con WolframAlpha si può
dare un'occhiata ad alcune opere di Piero della Francesca
artworks of Piero della Francesca
oltre che approfondire il tema delle proiezioni geometriche
mathworld subject map projections
|
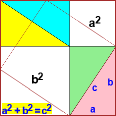 | |
Oltre ai gif animati posso realizzare animazioni concatenando pagine che contengano immagini differenti e che siano apribili, una dopo l'altra, premendo un tasto:
vedi "Pitagora_teorema" accessibile da qui. Questo è solo un esempio. Altre animazioni possono essere usate in matematica e in altre discipline per facilitare o stimolare la comprensione affiancando (o precedendo) argomentazioni verbali.
|
15 Altro aspetto che vede l'intreccio tra matematica e rappresentazioni figurative è costituito dal tema dei
paradossi della visione. Qualche esempio (rette parallele che non sembrano tali, rette che non sembrano rettilinee):

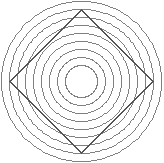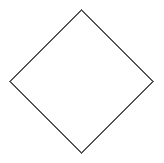

16 Esempio significativo del rapporto tra matematica e arti figurative è anche il tema delle tassellazioni.
| Un mosaico dell'antica Roma | |
 |
Il problema era come costruire tassellazioni che non fossero realizzate con poligoni regolari.
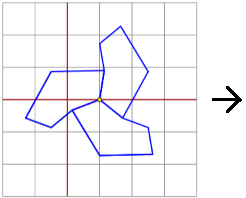
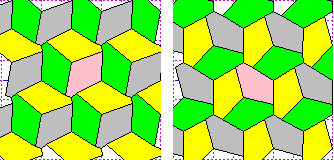
Una soluzione venne ideata (e dimostrata) dal cristallografo Friedrich Haag (non da un matematico), nel 1923. Qualche esempio:
Vediamo l'illustrazione della cosa con lo script animato Escher a cui si accede da qui (clicca più volte "riavvia").
Per una illustrazione del teorema di Haag (noto come teorema di Escher, che lo utilizzò per alcune famose tassellazioni), e una sua dimostrazione, vedi il collegamento a cui si accede dallo script precedente.
17 Nella scuola di base come far capire
in che modo sono realizzate le immagini digitali?
 | | Occorre dare l'idea che queste immagini sono costituite da tanti piccoli quadretti (vedi la figura seguente - un pezzo di girasole), e dare l'idea di come col computer si possano tracciare immagini digitali.
Prima di usare Paint o altri software per tracciare immagini può essere utile, nella scuola di base, ricorrere ad un programmino come
questo.
 |
Nella scuola superiore si potrà esplorare la matematica incorporata nelle più semplici applicazioni grafiche per tracciare figure di vario tipo. Consideriamo un esempio affrontabile alla fine delle superiori, che l'insegnante potrebbe anche utilizzare come uno degli spunti per avviare il calcolo differenziale.
Come fa una applicazione grafica per computer a realizzare le tangenti a una curva? o, viceversa, a tracciare, data una certa retta e un certo punto, una curva che in quel punto abbia tale retta come tangente?
Consideriamo ad es. il tracciamento di tratti curvilinei usando  o
o
 in Paint o usando "bottoni", menu o comandi simili in altri tipi di applicazioni:
in Paint o usando "bottoni", menu o comandi simili in altri tipi di applicazioni:
(1) si individuano, cliccando, due punti P e Q; appare un segmento che li ha come vertici; (2) si clicca su un punto P1; il segmento si incurva nella direzione di esso; (3) se poi clicco su un altro punto P2 la curva si deforma ulteriormente, in modo tale da assumere un andamento che richiama la forma della spezzata P P1P2Q
| (3) |  | 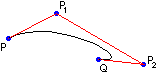 |
| Osservando le figure si intuisce che la curva si dispone prima in modo che i segmenti PP1 e QP1 siano tangenti alla curva in P e Q, poi in modo che lo siano i segmenti PP1 e QP2. Questa osservazione è confermata se si clicca sul punto P2 nel modo illustrato a lato: la curva viene tirata verso P1 e verso P2 in modo che PP1 sia tangente in P e QP2 lo sia in Q. | (3')  | 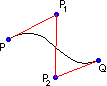 |
Come fa questo programma a comportarsi in questo modo?
Che cosa vuol dire per esso che una retta sia tangente a una curva? [curve di questo tipo sono chiamate curve di Bezier, dal nome dell'ingegnere francese Pierre Étienne Bezier che le ha ideate per disegnare il profilo di alcuni modelli delle automobili Renault:
una dei tanti esempi di interscambio tra matematica e altri "mondi"].
18 La statistica è la prima attività matematica intrapresa dall'uomo, è una delle prime affrontabili a scuola ed è, tipicamente, utilizzata in contesti non matematici.

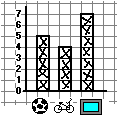
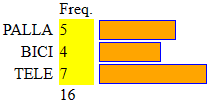
Dopo gli istogrammi a quadretti, utilizzabili sin dalla scuola dell'infanzia, nella scuola di base si può
introdurre anche l'uso dei mezzi di calcolo. Sopra a destra l'istogramma realizzato con il semplice script istogramma a barre
presente qui (introducendo via via: PALLA 5 BICI 4 TELE 7). Altri esempi:

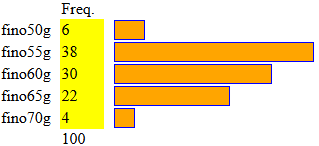
100 uova di razza livornese così suddivise:
6 uova fino a 50 g, altre 38 fino a 55, altre
30 fino a 60, altre 22 fino 65, altre 4 fino 70 |
 |
Quello a sinistra è un altro istogramma di dati già classificati. Dopo aver capito come siano realizzati gli istogrammi, si possono
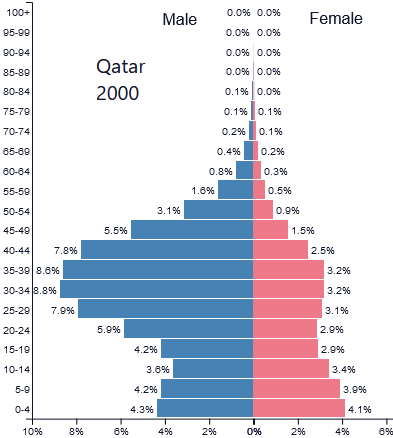
consultare anche siti che li utilizzano, come il bellissimo populationpyramid (sopra l'istogramma
della popolazione nel 2000 del Quatar - come mai sono così diverse la distribuzione per età degli uomini e quella delle donne?). Istogrammi della popolazione simili sono realizzabili anche con WolframAlpha.
Si possono, poi, utilizzare dei software che permettono di tracciare istogrammi di dati da classificare, anche in grandi quantità. Esiste il classico software libero R, impiegabile nella scuola secondaria di 2º grado. Altrimenti si possono usare dei semplici script come il seguente, con cui vediamo, ad esempio, come si possono analizzare alcune migliaia di dati
(questi) relativi al peso dei maschi ventenni in Italia:
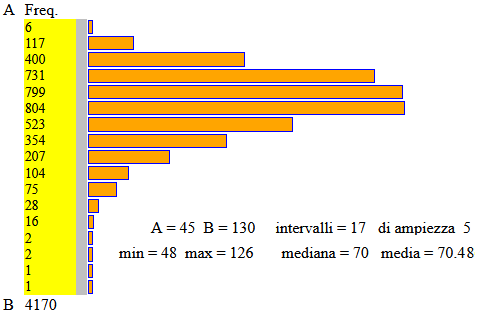
Potremmo fare esempi di impiego della statistica in ogni area disciplinare.
19 Vediamo ora qualche esempio di impiego del software matematico in geografia.
Con WolframAlpha (mathworld subject map projections):

La distanza ortodromica, cioè la distanza tra 2 punti su una sfera, con
questo script.
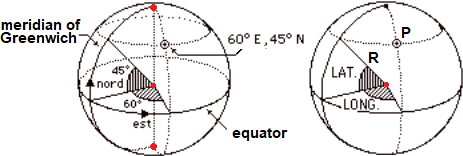
La distanza tra Genova (44.42 N, 8.93 E) e Sydney (33.87 S, 151.2 E), tenendo conto della lunghezza del raggio terrestre (circa 6370 km),
è di 16600 km.
| |  |
20 Il calcolo approssimato è un'altra area della
matematica che ha interazioni con le altre discipline e, soprattutto, con la fisica. Nel caso delle operazioni elementari è facile fare i calcoli, ma dispendioso in termini di tempo, anche usando una calcolatrice. Cosa si può con un semplice script, come
questo, che non fa altro che automatizzare i calcoli:
 |
|
Un'automobile, mentre sta viaggiando a velocità costante, percorre una distanza di 240 ± 2 m in 12 ± 0.2 s. Qual è la sua velocità?
<===
20.01 ± 0.50 m/s, or 20 ± 0.5 m/s. |
I calcoli si potrebbero fare anche con WolframAlpha (facciamolo):
minmax x/y if (238 < x < 242, 11.8 < y < 12.2)
min ≈ 19.5082 at (x,y) = (238, 12.2)
max ≈ 20.5085 at (x,y) = (242, 11.8)
L'intervallo che ha per estremi l'approssimazione per difetto e l'approssimazione per eccesso viene detto intervallo di indeterminazione di X e l'ampiezza di questo intervallo viene chiamata indeterminazione (o incertezza) di X: quanto più piccola è l'indeterminazione tanto meno indeterminata (cioè tanto più precisa) è la nostra conoscenza di X.
[in qualche manuale scolastico di fisica si trova l'impiego - in malo modo - di formule
"strane" che agli alunni "pensanti" non possono che apparire come "buffe": vedi]
21 Abbiamo fatti molti esempi per dare un'idea delle interazioni
possibili tra matematica ed altre discipline, interazioni che a scuola possono essere affrontate più facilmente e con maggiori stimoli
per gli alunni se si ricorre ai sussidi tecnologici. Gli esempi potrebbero essere molti altri. Qualche flash lo potete trovare in
questo documento in cui vengono richiamati anche alcuni impieghi non matematici di
WolframAlpha.
Vedi anche QUI
22 Proviamo a fare una sintesi.
In questi tre incontri abbiamo visto molti esempi di gestione delle risorse informatiche. Si è visto come possono
essere impiegate in molti contesti culturali. Uno degli obiettivi degli incontri era mettere in guardia dai
rischi che molte delle attività di aggiornamento o formazione sul "coding", mistificando il ruolo del "coding" (ossia della
"programmazione"), tendono a ridurlo ad una attività di gioco, scissa dagli insegnamenti-apprendimenti di cui si occupano
le varie discipline. Questo accade un po' per scelta, un po' per ignoranza degli "obiettivi dell'educazione scolastica" di chi le conduce.
La cosa tragica è che questa impostazione del "coding" è ben accolta da non pochi docenti delle varie
discipline, che non vogliono mettere in discussione le proprie pratiche didattiche e inserire interazioni disciplinari con l'impiego dei
mezzi di calcolo e, più in generale, attività volte ad educare alla consultazione di "Internet" e all'uso
consapevole delle risorse informatiche liberamente accessibili. Preferiscono
fare affidamento su (costosissimi) libri di testo che, in molti casi, sono in contrasto con le indicazioni ministeriali e fanno riferimento
ad un uso ghettizzato delle nuove tecnologie, a volte facendo riferimento ad autarchici software allegati.
Perché non educare gli alunni a selezionare e ad usare consapevolmente le risorse informatiche?
Per altri script vedi QUI, per altri esempi d'uso di WolframAlpha
vedi QUI.







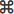 -Option-U nei Mac), od anche usando il menu View/Visualizza o comandi simili del browser, come si può fare con tutti i documenti Html.
Per accedere direttamente al codice sorgente (ed eventualmente modificarlo) si può aprire il file con Blocco_Note o
un altro editor di testi. In questo caso devo aprire https://www.macosaweb.it/script/divisori.htm (devo mettere ciò nella casella
che si apre azionado il comando "Apri" o "Open" o …)
-Option-U nei Mac), od anche usando il menu View/Visualizza o comandi simili del browser, come si può fare con tutti i documenti Html.
Per accedere direttamente al codice sorgente (ed eventualmente modificarlo) si può aprire il file con Blocco_Note o
un altro editor di testi. In questo caso devo aprire https://www.macosaweb.it/script/divisori.htm (devo mettere ciò nella casella
che si apre azionado il comando "Apri" o "Open" o …)
















 o
o
 in Paint o usando "bottoni", menu o comandi simili in altri tipi di applicazioni:
in Paint o usando "bottoni", menu o comandi simili in altri tipi di applicazioni: